Percepatan Sudut Dalam Gerak Melingkar

Mungkin kamu pernah menaiki sepeda ke sekolah, selama perjalanan gerak roda sepeda tidak mungkin memiliki kecepatan sudut yang tetap. Roda sepeda kadang berputar pelan karena harus menghindari rintangan atau kadang berputar lebih cepat karena melewati jalan lurus tanpa hambatan. Bahkan, roda kadang harus berhenti karena menunggu teman akan berangkat ke sekolah.

Perubahan kecepatan sudut pada roda sepeda tersebut menunjukkan besarnya percepatan sudut yang terjadi pada roda sepeda. Oleh karena kecepatan sudut dari suatu gerak melingkar tidak selalu tetap, dikenal istilah percepatan sudut. Percepatan sudut menunjukkan adanya perubahan kecepatan sudut dalam suatu selang waktu tertentu. Dengan demikian percepatan sudut atau percepatan anguler adalah perubahan kecepatan sudut yang terjadi tiap satuan waktu. Semakin besar perubahan kecepatan sudut pada gerak melingkar maka semakin besar pula percepatan sudutnya. Demikian juga sebaliknya, semakin besar pengurangan kecepatan sudut pada gerak melingkar maka semakin besar nilai perlambatan sudut dari gerak melingkar itu. Sama seperti kecepatan sudut (kecepatan anguler), pada percepatan sudut ada dua yakni percepatan rata-rata dan percepatan sesaat.

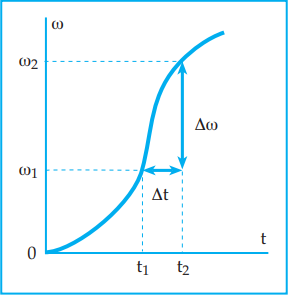
Percepatan sudut rata-rata adalah hasil bagi perubahan kecepatan sudut dengan selang waktu yang ditempuh. Secara matematis percepatan rata-rata dapat dirumuskan:

 

α_R = Δω/Δt

 

dimana:

Δω = ω₂ – ω₁

Δt = t₂ – t₁

 

Sehingga persamaan percepatan sudut rata-rata dapat dituliskan:

 

α_R = (ω₂ – ω₁)/(t₂ – t₁)

 

Keterangan:

α_R : percepatan sudut rata-rata (rad²/s)

Δω : perubahan kecepatan sudut (rad/s)

Δt : selang waktu yang ditempuh (s)

ω₁ : kecepatan sudut awal (rad/s)

ω₂ : kecepatan sudut akhir (rad/s)

t₁ : waktu awal (s)

t₂ : waktu akhir (s)

 

sedangkan percepatan sudut sesaat adalah percepatan rata-rata dengan nilai dt sangat kecil sekali atau Δt mendekati nol. Percepatan sudut sesaat dirumuskan sebagai berikut.

 

α = dω /dt

 

berdasarkan persamaan tersebut, percepatan sudut sesaat adalah turunan pertama dari percepatan sudut, atau dapat pula ditentukan dari turunan kedua dari posisi sudut. Percepatan sudut sesaat dapat pula ditentukan dari kemiringan garis singgung grafik kecepatan sudut terhadap waktu.

 

Pada gerak melingkar, kecepatan sudut suatu benda dapat ditentukan dari percepatan sudut dengan cara mengintegralkannya. Jadi, jika kecepatan sudut awal diketahui ω_o dan percepatan sudut suatu gerak melingkar berubah beraturan α diketahui maka kecepatan sudut sesaatnya dinyatakan dengan persamaan:

 

ω = ω_o + ꭍαdt

 

dengan:

ω = kecepatan sudut pada saat t (rad/s)

ω_o = kecepatan sudut awal (rad/s)

α = percepatan sudut (rad/s²)

t = waktu (s)

 

Secara matematis, nilai integral suatu fungsi juga menunjukkan luas daerah di bawah kurva maka kecepatan sudut pun dapat ditentukan dengan menghitung luas grafik antara percepatan terhadap waktu. Dengan demikian, metode grafik dapat digunakan sebagai suatu alternatif penentuan kecepatan sudut.

 

Posisi sudut dapat dicari dari fungsi kecepatan sudut sesaat. Apabila kecepatan sudut suatu benda diketahui, kita dapat menentukan fungsi posisi benda dengan mengintegralkan fungsi kecepatan sudut tersebut yang dapat dinyatakan dengan persamaan:

 

θ = θ_o + ꭍω dt

 

dengan:

θ = posisi sudut pada saat t (rad)

θ_o = posisi sudut awal (rad)

ω = kecepatan sudut (rad/s)

t = waktu (s)

 

Nah untuk memantapkan memahami materi percepatan sudut dalam gerak melingkar, silahkan simak contoh soal di bawah ini.

 

Contoh Soal 1

Sebuah roda berotasi pada suatu poros tertentu. Titik partikel pada roda tersebut memenuhi persamaan kecepatan sudut ω = 2t² – 3t + 8, dengan ω dalam rad/s dan t dalam sekon. Tentukanlah: (a). percepatan sudut rata-rata partikel untuk selang waktu t = 2 sekon sampai t = 6 sekon, (b). percepatan sudut awal partikel, dan (c). percepatan sudut partikel pada saat t = 6 sekon.

 

Penyelesaian:

ω = 2t² – 3t + 8

 

(a) kecepatan sudut pada saat t = 2 s yakni:

ω = 2t² – 3t + 8

ω₂ = 2(2)² – 3(2) + 8

ω₂ = 8 – 6 + 8

ω₂ = 10 rad/s

 

kecepatan sudut pada saat t = 6 s yakni:

ω = 2t² – 3t + 8

ω₆ = 2(6)² – 3(6) + 8

ω₆ = 72 – 18 + 8

ω₆ = 62 rad/s

 

percepatan rata-rata pada saat t = 2 s hingga t = 6 s yakni:

α_R = (ω₆ – ω₂)/(t₆ – t₂)

α_R = (62 – 10)/(6 – 2)

α_R = 52/4

α_R = 13 rad/s²

 

(b). Persamaan percepatan sudut partikel yakni:

α = dω/dt

α = d(2t² – 3t + 8)/dt

α = 4t – 3

 

percepatan awal pada saat t = 0, maka:

α = 4t – 3

α = 4(0) – 3

α = – 3 rad/s²

 

(c). percepatan sudut partikel pada saat t = 6 sekon yakni:

α = 4t – 3

α = 4(6) – 3

α = 21 rad/s²

 

Contoh Soal 2

Posisi sudut suatu titik pada roda dinyatakan oleh persamaan θ = 2t³ – 3t² + 6, dengan θ dalam rad dan t dalam sekon. Tentukanlah percepatan sudut pada saat t = 2 sekon.

 

Penyelesaian:

θ = 2t³ – 3t² + 6

 

Untuk mencari percepatan sesaat dengan cara menurunkan (diferensial) persamaan posisi sudut maka:

ω = dθ/dt

ω = d(2t³ – 3t² + 6)/dt

ω = 6t² – 6t

 

diferensialkan persamaan kecepatan sudut yakni:

α = dω/dt

α = d(6t² – 6t)/dt

α = 12t – 6

 

percepatan sudut partikel pada saat t = 2 sekon yakni:

α = 12t – 6

α = 12(2) – 6

α = 24 – 6

α = 18 rad/s²

 

Bagaimana? Mudah bukan? Jika ada permasalahan mengenai materi percepatan sudut dalam gerak melingkar silahkan tanyakan dikolom komentar.

TOLONG DIBAGIKAN YA :