Menentukan Tinggi Maksimum pada Gerak Parabola

Pada postingan sebelumnya Mafia Online sudah membahas tentang menentukan waktu untuk mencapai tinggi maksimum. Nah postingan kali ini akan membahas tentang cara menentukan tinggi maksimum pada gerak parabola.

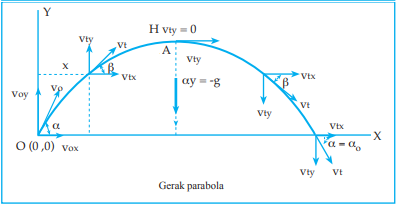
Perhatikan gambar di bawah ini.

Pada gerak parabola, pada saat benda mencapai ketinggian maksimum (di titik A) benda akan diam sesaat (kecepatan arah vertikal sama dengan 0), sehingga:

v_y = 0

dalam hal ini v_y = v_o sin α – gt, sehingga:

0 = v_o sin α – gt

gt = v_o sin α

t = (v_o sin α)/g

dengan t adalah waktu untuk mencapai ketinggian maksimum.

Pada gerak parabola, untuk menentukan posisi benda pada sumbu-y (menurut ketinggian) dapat dituliskan dengan persamaan berikut:

 

y_t = v₀ sin α . t – ½ gt²

 

Jika t kita substitusikan ke persamaan y_t = v₀ sinα . t – ½ gt², maka:

y_t = v₀ sin α . t – ½ gt²

y_t = v₀ sin α . (v_o sin α)/g – ½ g[(v_o sin α)/g]²

y_t = v₀² sin² α/g – ½ v₀² sin² α/g

y_t = v₀² sin² α/2g

 

Jadi untuk menentukan tinggi maksimum pada gerak parabola dapat menggunakan persamaan:

 

y_t = v₀² sin² α/2g

 

 

Untuk memantapkan pemahaman kamu tentang materi menentukan tinggi maksimum pada gerak parabola, silahkan simak contoh soal di bawah ini.

 

Contoh Soal 1

Sebuah peluru ditembakkan dengan kecepatan awal 40 m/s dan sudut elevasi 30°. Tentukan tinggi maksimum (g = 10 m/s²)!

 

Jawab:

v_o = 40 m/s

α = 30°

g = 10 m/s²

 

Untuk mengerjakan soal di atas bisa dilakukan dengan 2 cara yakni:

 

Cara 1

Kamu harus mencari terlebih dahulu waktu yang diperlukan oleh peluru untuk mencapai titik tertinggi (tinggi maksimum) yakni:

t = (v_o sin α)/g

t = (40 sin 30°)/10

t = 2 s

 

Sekarang cari tinggi maksimum dengan cara mensubtitusi nilai t = 2 s ke persamaan:

y_t = v₀ sin α . t – ½ gt²

y_t = 40 sin 30° . 2 – ½ 10.2²

y_t = 40 – 20

y_t = 20 m

 

Cara 2

Untuk cara kedua ini bisa menggunakan rumus:

y_t = v₀² sin² α/2g

y_t = 40² sin² 30°/2(10)

y_t = 40² (0,5)²/20

y_t = 1600.0,25/20

y_t = 400/20

y_t = 20 m

Jadi, tinggi maksimum peluru tersebut adalah 20 meter.

 

Contoh Soal 2

Sebutir peluru ditembakkan dari senapan dengan kecepatan awal 100 m/s. Sudut elevasi saat itu sebesar 15° (sin 15° = 0,26). Hitunglah tinggi maksimum yang dapat dicapai peluru (g = 10 m/s²)!

 

Jawab:

V_o = 100 m/s

α = 15°

g = 10 m/s²

 

Untuk mencari tinggi maksimum yang dicapai oleh peluru dapat menggunakan rumus:

y_t = v₀² sin² α/2g

y_t = 100² sin² 15°/2(10)

y_t = 100² (0,26)²/2(10)

y_t = 10000.(0,0676)/20

y_t = 676/20

y_t = 33,8 m

Jadi tinggi maksimum yang dicapai oleh peluru adalah 33,8 meter.

 

Bagaimana? Mudah bukan? Untuk lebih memantapkan pemahaman kamu tentang cara mencari tinggi maksimum pada gerak parabola, silahkan kerjakan soal latihan di bawah ini, kemudian hasilnya dituliskan ke dalam kolom komentar.

Soal Latihan

Sebuah peluru yang memiliki kecepatan awal v₀ dan sudut elevasi 30°. Jika tinggi maksimum yang dicapai 30 m maka tentukan nilai v₀!

Selamat mengerjakan dan semoga berhasil.

TOLONG DIBAGIKAN YA :