Contoh Soal Menentukan Jarak Titik Ke Garis Pada Kubus

Sebelum menyimak contoh soal di bawah ini. Alangkah baiknya terlebih dahulu membaca materi tentang cara menentukan jarak titik ke garis pada bangun ruang kubus. Kalau sudah membaca materinya, silahkan lanjutkan simak contoh soal di bawah ini kemudian kerjakan soal latihannya.

 

Contoh Soal 1

Kubus PQRS.TUVW mempunyai panjang rusuk 6 cm. Titik A terletak di pertengahan rusuk RV. tentukan jarak titik V terhadap garis TA!

 

Pembahasan

Ilustrasikan terlebih dahulu soal tersebut ke dalam bangun ruang kubus, maka akan tampak seperti gambar di bawah ini.

 

Titik A berada di pertengahan RV sehingga :

AV = ¹/₂ x VR

AV = ¹/₂ x 6 cm

AV = 3 cm

 

Perhatikan ΔTUV!

TV² = TU² + UV²

TV² = 6² + 6²

TV² = 36 + 36

TV² = 72

TV =√72

TV = √36 x √2

TV = 6√2 cm

 

Selanjutnya perhatikan Δ AVT !

AT² = TV² + AV²

AT² = (6√2)² + 3²

AT² = 72 + 9

AT² = 81

AT =√81

AT = 9 cm

 

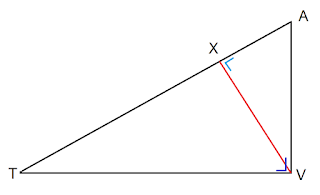
Tarik garis dari titik V tegak lurus garis TA! Tandai pertemuannya sebagai titik X! VX adalah yang merupakan garis tinggi ΔAVT yang merupakan jarak titik V terhadap garis TA, seperti gambar di bawah ini.

Luas ΔAVT = ¹/₂ x alas x tinggi, jika alasnya TV, maka luasnya:

Luas ΔAVT = ¹/₂ x TV x AV

Sedangkan jika alasnya AT, maka luasnya:

Luas ΔAVT = ¹/₂ x AT x VX

 

Jarak VX dapat dicari yakni:

Luas ΔAVT = Luas ΔAVT

½ x TV x AV = ½ AT x VX

TV x AV = AT x VX

6√2 x 3 = 9 x VX

18√2 = 9.VX

VX = 18√2/9

VX = 2√2

Jadi jarak titik V terhadap garis TA adalah 2√2 cm.

 

Contoh Soal 2

Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Titik P adalah titik potong AH dan ED dan titik Q adalah titik potong FH dan EG. Tentukan jarak titik B ke garis PQ

 

Penyelesaian:

Ilustrasikan terlebih dahulu soal tersebut ke dalam bangun ruang kubus, maka akan tampak seperti gambar di bawah ini.

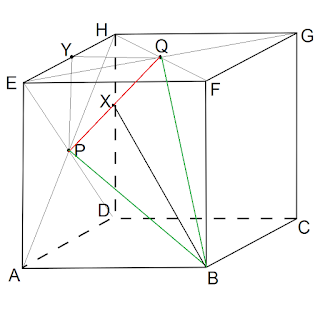
Jarak titik B ke garis PQ adalah BX.

AH = √(AE² + EH²)

AH = √(4² + 4²)

AH = √(16 + 16)

AH = √32

AH = 4√2 cm

 

PH = ½ AH

PH = ½ 4√2

PH = 2√2

 

PY = QY = ½ AB = 2 cm

 

PQ = √(PY² + QY²)

PQ = √(2² + 2²)

PQ = √8

PQ = 2√2 cm

 

ΔBPQ merupakan Δ sama kaki, maka:

PX = ½ PQ

PX = √2 cm

 

BP = √(AP² + AB²)

BP = √(2√2² + 4²)

BP = √(8 + 16)

BP = √24

BP = 2√6 cm

 

BX = √(BP² – PX²)

BX = √(2√6² – √2²)

BX = √(24 – 2)

BX = √22 cm

 

Bagaimana? Mudah bukan? Untuk memantapkan pemahaman kamu tentang materi menentukan jarak titik ke garis pada kubus, silahkan kerjakan soal latihan di bawah ini. Kemudian hasilnya tuliskan di kolom komentar.

 

Soal Latihan

Kubus ABCD.EFGH memiliki panjang rusuk 6 cm. Tentukan jarak titik B ke CE!

TOLONG DIBAGIKAN YA :