Contoh Soal dan Pembahasan Prisma Trapesium Part 2

Pada postingan sebelumnya Mafia Online sudah membahas tentang contoh soal prisma trapesium dan penyelesaiannya. Pada postingan tersebut hanya membahas tentang cara mencari volume dan luas permukaan prisma trapesium siku-siku. Sebenarnya pada bentuk prisma trapesium ada tiga jenis, yakni prisma trapesium siku-siku, prisma trapesium sama kaki, dan prisma trapesium sebarang.

Agar kamu lebih mudah memahami contoh soal di bawah ini, silahkan baca dan kuasai konsep di bawah ini terlebih dahulu:

• Pengertian, Jenis dan Sifat Trapesium
• Cara Mencari Keliling dan Luas Trapesium
• Pengertian, Jenis-Jenis dan Sifat-Sifat Prisma
• Cara Menghitung Volume Prisma
• Cara Menghitung Luas Permukaan Prisma

Jika sudah pernah membaca atau sudah paham dengan konsep tersebut, oke kita bahas satu persatu.

 

Prisma Trapesium Siku-Siku

Prisma Trapesium siku-siku adalah bangun ruang prisma yang bentuk alasnya berupa trapesium yang salah satu sudutnya merupakan sudut siku-siku (90°). Karena ada sudut siku-siku, kamu perlu memahami konsep segitiga siku-siku yaitu teorema Pythagoras jika itu diperlukan untuk menyelesaikan soal. Berikut admin bagikan contoh soal prisma trapesium siku-siku, silahkan pahami.

 

Perhatikan gambar prisma trapesium siku-siku di bawah ini!

Tentukan volume dan luas permukaan prisma trapesium siku-siku di atas!

 

Penyelesaian:

Pada gambar di atas merupakan bentuk bangun ruang prisma ABCD.EFGH dengan alasnya berbentuk trapesium ABCD. Untuk mencari volume (V) dari prisma dapat menggunakan rumus:

V = luas alas x tinggi

 

Luas alas (La) sama dengan luas trapesium maka:

La = ½ (AB + CD) x AD => (ingat** CD = GH)

La = ½ (10 cm + 16 cm) x 8 cm 

La = 104 cm²

 

Jadi volume prisma trapesium siku-siku yakni:

V = La x DH

V = 104 cm² x 20 cm

V = 2080 cm³

 

Sedangkan untuk mencari luas permukaan prisma trapesium siku-siku di atas Anda harus mencari keliling (K) trapesium ABCD. Sekarang perhatikan gambar di bawah ini.

 

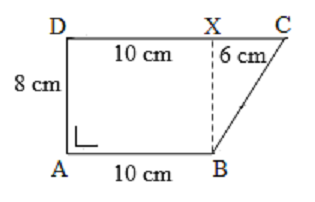
Agar diperoleh keliling trapesium tersebut Anda harus mencari panjang BC dengan menggunakan teorema Phytagoras, maka:

BC² = BX² + CX²

BC² = 8² + 6²

BC² = 64 + 36

BC² = 100

BC = √100

BC = 10 cm

 

Keliling trapesium ABCD yakni:

K = AB + BC + CD + AD

K = 10 cm + 10 cm + 16 cm + 8 cm

K = 44 cm

 

Untuk mencari luas permukaan (L) prisma trapesium siku-siku dapat menggunakan rumus:

L = (2 x luas alas) + (keliling x tinggi)

L = (2 x La) + (K x DH)

L = (2 x 104 cm²) + (44 cm x 20 cm)

L = 208 cm² + 880 cm2

L = 1088 cm²

 

Jadi, volume dan luas permukaan prisma pada gambar di atas adalah 2080 cm³ dan 1088 cm²

 

Prisma Trapesium Sama Kaki

Prisma trapesium sama kaki adalah bangun ruang prisma yang alasnya berbentuk trapesium yang mempunyai sepasang sisi yang sama panjang, di samping mempunyai sepasang sisi yang sejajar. Berikut admin bagikan contoh soal prisma trapesium sama kaki, silahkan pahami.

 

Perhatikan gambar prisma trapesium sama kaki di bawah ini! 

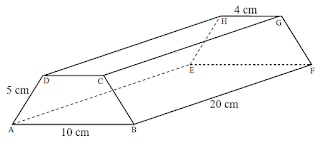
Tentukan volume dan luas permukaan prisma trapesium siku-siku di atas!

 

Penyelesaian:

Pada gambar di atas merupakan bentuk bangun ruang prisma ABCD.EFGH dengan alasnya berbentuk trapesium sama kaki. Untuk mencari volume (V) dari prisma di atas dapat kita gunakan rumus:

V = luas alas x tinggi

 

Cari telebih dahulu luas alas prisma yang berbentuk trapesium sama kaki. Tetapi kita cari terlebih dahulu tinggi trapesium. Perhatikan gambar trapesium sama kaki di bawah ini.

Tinggi trapesium ABCD merupakan garis DX atau CY (DX = CY). Panjang DX dapat di cari dengan menggunakan teorema Phytagoras, yakni:

DX² = AD² – AX²

DX² = 5² – 3²

DX² = 25 – 9

DX² = 16

DX = √16

DX = 4 cm

 

Luas alas (La) trapesium yakni:

La = ½ (AB + CD) x DX

La = ½ (10 cm + 4 cm) x 4 cm 

La = 28 cm²

 

Jadi volume prisma trapesium siku-siku di atas yakni:

V = La x BF

V = 28 cm² x 20 cm

V = 560 cm³

 

Keliling trapesium ABCD yakni:

K = AB + BC + CD + AD

K = 10 cm + 5 cm + 4 cm + 5 cm

K = 24 cm

 

Untuk mencari luas permukaan (L) prisma trapesium sama kaki dapat menggunakan rumus:

L = (2 x luas alas) + (keliling x tinggi)

L = (2 x La) + (K x BF)

L = (2 x 28 cm²) + (24 cm x 20 cm)

L = 56 cm² + 480 cm2

L = 536 cm²

 

Jadi, volume dan luas permukaan prisma pada gambar di atas adalah 560 cm³ dan 536 cm²

 

Prisma Trapesium Sebarang

Prisma trapesium sebarang adalah bangun ruang prisma yang alasnya berbentuk trapesium yang keempat sisinya tidak sama panjang. Berikut admin bagikan contoh soal prisma trapesium sebarang, silahkan pahami.

 

Perhatikan gambar prisma trapesium sama kaki di bawah ini!

Tentukan volume dan luas permukaan prisma trapesium sebarang di atas!

Penyelesaian:

Pada gambar di atas merupakan bentuk bangun ruang prisma ABCD.EFGH dengan alasnya berbentuk trapesium sebarang (semua sisi trapesium tidak sama). Untuk mencari volume (V) prisma trapesium sebarang dapat menggunakan rumus:

V = luas alas x tinggi

 

Cari telebih dahulu luas alas prisma yang berbentuk trapesium sebarang tersebut yakni:

La = ½ (AB + CD) x t

Ingat CD = HG, maka:

La = ½ (25 cm + 4 cm) x 8 cm 

La = 116 cm²

 

Jadi volume prisma trapesium sebarang dapat dihitung yakni:

V = La x BF

V = 116 cm² x 30 cm

V = 3480 cm³

 

Keliling trapesium ABCD yakni:

K = AB + BC + CD + AD

K = 25 cm + 10 cm + 4 cm + 17 cm

K = 56 cm

 

Untuk mencari luas permukaan (L) prisma trapesium sebarang dapat menggunakan rumus:

L = 2 x luas alas + keliling x tinggi

L = (2 x La) + (K x BF)

L = (2 x 116 cm²) + (56 cm x 30 cm)

L = 232 cm² + 1680 cm2

L = 1912 cm²

 

Jadi, volume dan luas permukaan prisma pada gambar di atas adalah 560 cm³ dan 536 cm²

 

Bagaimana? Mudah bukan? Demikian artikel Mafia Online tentang contoh soal dan pembahasan prisma trapesium bagian 2 lengkap dengan gambar dan penyelesaiannya. Mohon maaf jika ada kata atau tulisan yang salah pada postingan ini.

TOLONG DIBAGIKAN YA :