Cara Mencari Panjang Diagonal Ruang Balok

Diagonal ruang pada balok adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan dalam suatu bangun ruang balok. Pada bangun ruang balok terdapat empat buah diagonal ruang. Perhatikan gambar di bawah ini!

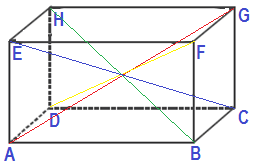
Gambar di atas merupakan sebuah bangun ruang balok ABCD. EFGH. Adapun diagonal ruang pada bangun balok ABCD.EFGH adalah garis AG, BH, CE, dan DF. Semua diagonal ruang pada balok memiliki panjang yang sama. Bagaimana cara mencari panjang diagonal ruang pada balok?

 

Untuk mencari panjang diagonal ruang pada balok kamu harus paham dengan konsep teorema Pythagoras. Sekarang perhatikan gambar di bawah ini.

Garis AG merupakan diagonal ruang pada balok ABCD.EFGH. Sekarang perhatikan segitiga ABC yang merupakan segitiga siku-siku. Panjang AC merupakan diagonal bidang ABCD yang dapat dicari dengan menggunakan teorema Pythagoras yakni:

AC² = AB² + BC²

AC² = p² + l²

b² = p² + l²

 

Sekarang cari panjang AG yang merupakan diagonal ruang balok ABCD.EFGH dengan menggunakan teorema Pythagoras yakni:

AG² = AC² + CG²

Ingat AC² = p² + l², maka:

d² = p² + l² + t²

d = √(p² + l² + t²)

 

Nah untuk memantapkan pemahaman kamu tentang cara mencari panjang diagonal ruang pada balok, silahkan simak contoh soal di bawah ini.

 

Contoh Soal

Diketahui balok ABCD.EFGH dengan panjang AB = 6 cm, BC = 8 cm, dan CG = 15 cm. Tentukan panjang diagonal ruang balok tersebut!

 

Penyelesaian:

Jika soal di atas diilustrasikan akan tempak seperti gambar di bawah ini.

Cari panjang BD dengan menggunakan Teorema Pythagoras yakni:

BD² = BC² + CD²

BD² = 8² + 6²

BD² = 100

BD = 10 cm

 

Cari panjang BH juga menggunakan Teorema Pythagoras yakni:

BH² = BD² + DH²

BH² = 10² + 15²

BH² = 100 + 225

BH² = 325

BH = √325

BH = 5√13 cm

 

Selain dengan menggunakan cara di atas, panjang diagonal balok juga dapat dicari dengan menggunakan rumus yakni:

d = √(p² + l² + t²)

d = √(8² + 6² + 15²)

d = √(64 + 36 + 225)

d = √325

d = 5√13 cm

Jadi panjang diagonal ruang balok tersebut adalah 5√13 cm

 

Contoh Soal 2

Diketahui sebuah balok memiliki panjang 20 cm, lebar 6 cm dan tinggi 8 cm. Tentukan panjang diagonal ruang balok tersebut!

 

Penyelesaian:

p = 20 cm

l = 6 cm

t = 8 cm

 

Panjang diagonal balok dapat dicari dengan menggunakan rumus:

d = √(p² + l² + t²)

d = √(20² + 6² + 8²)

d = √(400 + 36 + 64)

d = √500

d = 10√5 cm

Jadi, panjang diagonal ruang balok tersebut adalah 10√5 cm.

 

Bagaimana? Mudah bukan? Demikianlah artikel tentang cara mencari panjang diagonal balok lengkap dengan gambar ilustrasi dan contoh soalnya. Apabila terdapat kesalahan tanda, simbol, huruf maupun angka dalam perhitungan mohon dimaklumi. Terimakasih atas kunjungannya dan sampai jumpa di artikel berikutnya.

TOLONG DIBAGIKAN YA :