Apakah Ada Hubungan Antara Diagonal Ruang Dengan Bidang Diagonal Kubus

Sebelum mengetahui apakah ada hubungan antara diagonal ruang dengan bidang diagonal pada kubus, kamu harus paham terlebih dahulu apa sih pengertian diagonal ruang dan bidang diagonal pada kubus.

 

Oke kita bahas definisi diagonal ruang dan bidang diagonal terlebih dahulu. Diagonal ruang suatu kubus adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan dalam suatu ruang kubus. Sedangkan bidang diagonal suatu kubus adalah bidang yang dibatasi oleh dua rusuk dan dua diagonal bidang suatu bangun ruang kubus.

 

Sekarang perhatikan gambar di bawah ini.

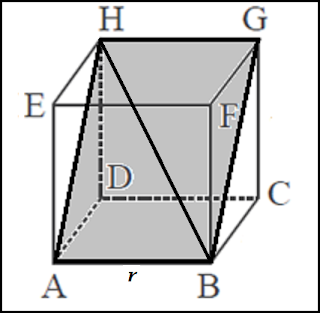Kubus ABCD.EFGH

Gambar di atas merupakan sebuah kubus ABCD.EFGH dengan panjang rusuk r, garis BH merupakan salah satu diagonal ruang kubus. Perlu diketahui bahwa pada kubus ada 4 buah diagonal ruang yang sama panjang. Panjang diagonal ruang dapat ditentukan dengan menggunakan rumus:

=> d_r = r√3

=> r = d_r/√3 . . . . . . . (1)

 

Sekarang perhatikan gambar di atas, lihat bidang ABGH. Bidang ABGH merupakan salah satu bidang diagonal kubus. Perlu diketahui ada 6 buah bidang diagonal pada kubus. Bidang diagonal pada kubus berbentuk persegi panjang, sehingga untuk mencari luas bidang diagonal kubus dapat dicari dengan menggunakan rumus:

L_d = rusuk x diagonal sisi

L_d = r x d_s . .  . . . . . . (2)

 

Diagonal sisi atau diagonal bidang (d_s) pada kubus dapat di cari dengan menggunakan rumus:

d_s = r√2 . . . . . . . . (3)

 

Dengan mensubtitusi persamaan 1 ke persamaan 3 maka diperoleh hubungan antara diagonal ruang dengan diagonal sisi, yakni:

d_s = r√2

d_s = (d_r/√3)√2

d_s = (d_r√6)/3 . . . . . (4)

 

Dengan mensubtitusi persamaan 3 ke persaman 2 maka diperoleh rumus untuk mencari luas bidang diagonal pada kubus yakni:

L_d = r²√2 . . . . . . . . (5)

 

Dengan mensubtitusi persamaan (1) ke persamaan (5), maka akan diperoleh:

L_d = r²√2

L_d = (d_r/√3)²√2 . . . .(6)

 

Jadi hubungan antara diagonal ruang dengan bidang diagonal dapat dirumuskan dengan persamaan:

L_d = (d_r/√3)²√2

 

Untuk memantapkan pemahaman kamu tentang hubungan antara diagonal ruang dengan bidang diagonal, silahkan simak contoh soal di bawah ini.

 

Contoh Soal

Sebuah kubus memiliki panjang diagonal ruang 4√3 cm. Tentukan luas bidang diagonal kubus tersebut.

 

Penyelesaian:

Ada dua cara untuk menyelesaikan soal di atas yaitu cara manual dan cara cepat (dengan rumus)

Cara I (cara manual)

Cari terlebih dahulu rusuk kubus tersebut yakni:

d_r = r√3

4√3 = r√3

r = 4 cm

 

Cari panjang diagonal sisi kubus yakni:

d_s = r√2

d_s = 4√2 cm

 

Terkahir cari luas bidang diagonal kubus yakni:

L_d = r x d_s

L_d = (4 cm)(4√2 cm)

L_d = 16√2 cm

 

Cara II (dengan rumus)

Dengan menggunakan rumus hubungan antara diagonal ruang dengan bidang diagonal yakni:

L_d = (dr/√3)²√2

L_d = (4√3/√3)²√2

L_d = (4)²√2

L_d = 16√2 cm²

Jadi baik dengan menggunakan cara I maupun cara II, hasilnya akan tetap sama yakni luas bidang diagonal pada kubus tersebut sebesar 16√2 cm².

 

Berdasarkan pemaparan dan contoh soal di atas, maka dapat ditarik kesimpulan bahwa ada hubungan antara diagonal ruang dengan bidang diagonal pada kubus yang dapat dirumuskan dengan persamaan:

L_d = (d_r/√3)²√2

 

dengan:

L_d = luas bidang diagonal

d_r = panjang diagonal ruang

 

Demikian artikel tentang hubungan antara diagonal ruang dengan bidang diagonal pada kubus, lengkap dengan gambar ilustrasi dan contoh soal serta penyelesaian contoh soal tersebut. Mohon maaf jika ada kata atau tulisan yang salah dalam postingan ini.

TOLONG DIBAGIKAN YA :