Selisih dan komplemen dua himpunan => Pada postingan sebelumnya Mafia Online sudah membahas tentang operasi himpunan yakni irisan himpunan dan gabungan himpunan. Pada postingan kali ini masih mengulas tentang operasi himpunan yakni selisih dan komplemen dua himpunan. Apa itu selisih dua himpunan? Apa itu komplemen dua himpunan?
Selisih (Difference) Dua Himpunan
Selisih
(difference) himpunan A dan B adalah himpunan yang anggotanya semua anggota
dari A tetapi bukan anggota dari B. Selisih himpunan A dan B dinotasikan dengan
A – B atau A\B. Dengan
notasi pembentuk himpunan dituliskan sebagai berikut.
Catatan: A – B = A\B dibaca: selisih A dan B.
Selisih A dan B tidak sama dengan selisih B dan A. Untuk membuktikan hal tersebut silahkan simak selisih dua himpunan berikut ini. Misalkan himpunan A = {a, b, c, d} dan himpunan B = {a, c, f, g}. Maka:
Selisih A dan B adalah A – B = {a, b, c, d} – {a, c, f, g} = {b, d},
Selisih B dan A adalah B – A = {a, c, f, g} – {a, b, c, d} = {f, g}.
Jadi berdasarkan pemaparan di atas bahwa A - B tidak sama dengan B - A. Untuk memantapkan pemahaman Anda tentang selisih dua himpunan silahkan simak contoh soal tentang selisih himpunan di bawah ini.
Contoh Soal 1
Selisih A dan B adalah A – B = {a, b, c, d} – {a, c, f, g} = {b, d},
Selisih B dan A adalah B – A = {a, c, f, g} – {a, b, c, d} = {f, g}.
Jadi berdasarkan pemaparan di atas bahwa A - B tidak sama dengan B - A. Untuk memantapkan pemahaman Anda tentang selisih dua himpunan silahkan simak contoh soal tentang selisih himpunan di bawah ini.
Contoh Soal 1
Diketahui
S = {1, 2, 3, ..., 10} adalah himpunan semesta. Jika P = {2, 3, 5, 7} dan Q =
{1, 3, 5, 7, 9}, tentukan
a.
anggota S – P;
b.
anggota P – Q;
c.
anggota Q – P.
Penyelesaian:
a. S –
P = {1, 2, 3, ..., 10} – {2, 3, 5, 7} = {1, 4, 6, 8, 9, 10}
b. P –
Q = {2, 3, 5, 7} – {1, 3, 5, 7, 9} = {2}
c. Q –
P = {1, 3, 5, 7, 9} – {2, 3, 5, 7} = {1, 9}.
Komplemen Suatu Himpunan
Untuk lebih memudahkan memahami konsep komplemen himpunan maka konsep dasar yang Anda harus kuasai adalah konsep himpunan semesta atau semesta pembicaraan.
Komplemen himpunan A didefiniiskan sebagai suatu himpunan yang anggota-anggotanya merupakan anggota S tetapi bukan
anggota A. Dengan notasi pembentuk himpunan dituliskan sebagai berikut.
Misalkan diketahui S = {1, 2, 3, 4, 5, 6, 7} adalah himpunan semesta dan A = {3, 4, 5}. Komplemen himpunan A adalah AC = {1, 2, 6, 7}.
Komplemen
A dinotasikan dengan AC atau A’ (AC
atau A’ dibaca: komplemen A). Untuk memantapkan pemahaman Anda tentang komplemen suatu himpunan silahkan simak contoh soal tentang
Contoh
Soal 2
Diketahui
S = {1, 2, 3, ..., 10} adalah himpunan semesta. Jika A = {1, 2, 3, 4} dan B =
{2, 3, 5, 7}, tentukan
a.
anggota AC
b.
anggota BC
Penyelesaian:
Diketahui:
S = {1,
2, 3, 4, 5, 6, 7, 8, 9 10}
A = {1,
2, 3, 4}
B = {2,
3, 5, 7}
a. AC
= {5, 6, 7, 8, 9, 10}
b. BC
= {1, 4, 6, 8, 9, 10}
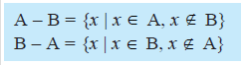







kalau yang soal komplemen himpunannya begini : AnBc (ngga pake tanda kurung tutup&buka) bagaimana caranya?
BalasHapusAnBc berarti maksudnya A irisan komplemen B. caranya kamu cari dulu komplemen Bnya, baru lakukan A irisan komplemen B itu
Hapusmakasih gan.. ulangan ane dapet seratus.. belajar ini malamnya.. eh gk nyadar klo dpet nilai 100
BalasHapusSelamat ya gan. Pertahankan terus prestasinya. Terima kasih atas kunjungannya.
Hapusthanks
BalasHapusComplemen dengan selisih koq susah bedainnya ya.... tlg donk cara mudahnya....
BalasHapusMakasih bgt ya.....
BalasHapusBerkat mbaca ini jd tambah ngerti materi ini dan g dapet hukuman gr2 enggak ngerkain pr
Mantap, terus posting hal yg positif dan bermanfaat untuk orang banyak👍👍👍
BalasHapus