Semua contoh soal di bawah ini Mafia Online ambil dari
soal-soal Ujian Nasional (UN). Dengan mempelajari contoh soal di bawah ini Anda
sudah punya bayangan bagaimana bentuk-bentuk soal yang keluar pada UN.
Selain itu Anda juga bisa memprediksikan bentuk-bentuk soal yang akan keluar
UN nantinya.
Contoh
Soal 1
Perhatikan gambar di bawah ini
Besar ∠ABD adalah ….
A. 98°
B. 105°
C. 112°
D. 119°
(UN 2008/2009)
Penyelesaian:
Untuk menjawab soal ini hal pertama yang Anda
cari adalah nilai x. Dalam hal ini ∠ABD dan ∠CBD merupakan sudut saling pelurus, maka:
∠ABD + ∠CBD = 180°
7x° + 5x° = 180°
12x° = 180°
x = 15°
∠ABD = 7x°
∠ABD = 7. 15°
∠ABD = 105°
Jadi, besar ∠ABD adalah 105° (Jawaban B)
Contoh
Soal 2
Perhatikan gambar di bawah ini
Nilai y adalah ….
A. 24°
B. 25°
C. 26°
D. 34°
(UN 2008/2009)
Penyelesaian:
Untuk menjawab soal ini Anda harus paham konsep
hubungan antarsudut jika dua garis sejajar dipotong oleh garis lain. Dalam hal
ini ∠CEF
dan ∠EAH
merupakan sudut sehadap, maka:
∠EAH = ∠CEF
∠EAH = 102°
∠EAH + ∠BAE = 180° (sudut saling berpelurus)
102°+ 3y = 180°
3y = 180°
- 102°
3y = 78°
y = 26° (Jawaban B)
Contoh
Soal 3
Besar pelurus sudut SQR adalah ….
A. 101°
B. 100°
C. 95°
D. 92°
(UN 2012/2013 paket 54)
Penyelesaian:
Perhatian** soal ini merupakan soal jebakan,
banyak yang mengira kalau soal tersebut menanyakan ∠SQR padahal yang diminta adalah ∠PQS. Untuk
menjawab soal ini hal pertama yang Anda cari adalah nilai x. Dalam hal ini ∠PQS
dan ∠SQR
merupakan sudut saling pelurus, maka:
∠PQS + ∠SQR = 180°
(5x)° + (4x+9)° = 180°
9x° + 9 = 180°
9x° = 171°
x° = 19°
Pelurus ∠SQR = ∠PQS
Pelurus ∠SQR = (5x)°
Pelurus ∠SQR = (5.19)°
Pelurus ∠SQR = 95° (Jawaban
C)
Contoh
Soal 4
Perhatikan gambar berikut
Besar sudut nomor 1 adalah 95°, dan besar sudut
nomor 2 adalah 110°. Besar sudut nomor 3 adalah ….
A. 5°
B. 15°
C. 25°
D. 35°
(UN 2009/2010 paket 10)
Penyelesaian:
∠1 = ∠5
= 95°
(sudut dalam berseberangan)
∠2 + ∠6
= 180° (saling berpelurus)
110° + ∠6
= 180°
∠6 = 70°
∠5 + ∠6
+ ∠3 = 180°
95° + 70°
+ ∠3 = 180°
165° + ∠3
= 180°
∠3 = 15°
(Jawaban B)
Contoh
Soal 5
Besar ∠BCA adalah ….
A. 70°
B. 100°
C. 110°
D. 154°
(UN 2010/2011 paket 15)
Penyelesaian:
∠ABC + ∠CBD
= 180° (saling berpelurus)
∠ABC + 112°
= 180°
∠ABC = 68°
∠BCA + ∠ABC
+ ∠BAC = 180°
∠BCA + 68°
+ 42° = 180°
∠BCA + 110
= 180°
∠BCA = 70°
(Jawaban A)
Contoh
Soal 6
Perhatikan gambar di bawah ini
Besar ∠P3 adalah ….
A. 37°
B. 74°
C. 106°
D. 148°
(UN 2010/2011 paket 15)
Penyelesaian:
∠P2 = 74° (sudut
luar berseberangan)
∠P2 + ∠P3
= 180° (saling berpelurus)
74° + ∠P3
= 180°
∠P3 = 106°
(Jawaban C)
Contoh
Soal 7
Besar pelurus sudut KLN adalah ….
A. 31°
B. 72°
C. 85°
D. 155°
(UN 2012/2013 paket 1)
Penyelesaian:
Untuk menjawab soal ini hal pertama yang Anda
cari adalah nilai x. Dalam hal ini ∠KLN dan ∠MLN merupakan sudut saling pelurus, maka:
∠KLN + ∠MLN = 180°
(3x + 15)° + (2x+10)°
= 180°
5x° + 25° = 180°
5x° = 155°
x° = 31°
Pelurus ∠KLN = ∠MLN
Pelurus ∠KLN = (2x+10)°
Pelurus ∠KLN = (2.31 + 10)°
Pelurus ∠KLN = 72° (Jawaban
B)
Contoh
Soal 8
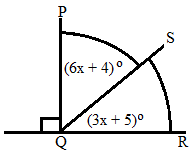
Perhatikan gambar di bawah ini
Besar penyiku ∠SQR adalah ….
A. 9°
B. 32°
C. 48°
D. 58°
(UN 2012/2013 paket 2)
Penyelesaian:
Perhatian** soal ini merupakan soal jebakan juga,
banyak yang mengira kalau soal tersebut menanyakan ∠SQR padahal yang diminta adalah ∠PQS. Untuk
menjawab soal ini hal pertama yang Anda cari adalah nilai x. Dalam hal ini ∠SQR
dan ∠PQS
merupakan sudut saling berpenyiku, maka:
∠SQR + ∠PQS = 90°
(3x + 5)° + (6x+4)°
= 90°
9x° + 9° = 90°
9x° = 81°
x° = 9°
Penyiku ∠SQR = ∠PQS
Penyiku ∠SQR = (6x+4)°
Penyiku ∠SQR = (6.9 + 4)°
Penyiku ∠SQR = 58° (Jawaban
D)
Contoh
Soal 9
Besar pelurus ∠AOC adalah ….
A. 32°
B. 72°
C. 96°
D. 108°
(UN 2012/2013 paket 5)
Penyelesaian:
Untuk menjawab soal ini hal pertama yang Anda
cari adalah nilai x. Dalam hal ini ∠AOC dan ∠BOC merupakan sudut saling pelurus, maka:
∠AOC + ∠BOC = 180°
(8x - 20)° + (4x+8)°
= 180°
12x° - 12° = 180°
12x° = 192°
x° = 16°
Pelurus ∠AOC = ∠BOC
Pelurus ∠AOC = (4x+8)°
Pelurus ∠AOC = (4.16 + 8)°
Pelurus ∠AOC = 72° (Jawaban
B)
Contoh
Soal 10
Besar penyiku ∠AQC adalah ….
A. 49°
B. 44°
C. 66°
D. 80°
(UN 2012/2013 paket 6)
Penyelesaian:
Untuk menjawab soal ini hal pertama yang Anda
cari adalah nilai x. Dalam hal ini ∠AQC dan ∠BQC merupakan sudut saling berpenyiku, maka:
∠AQC + ∠BQC = 90°
(6x + 4)° + (5x+9)°
= 90°
11x° + 13° = 90°
11x° = 77°
x° = 7°
Penyiku ∠AQC = ∠BQC
Penyiku ∠AQC = (5x+9)°
Penyiku ∠AQC = (5.7 + 9)°
Penyiku ∠AQC = 44° (Jawaban
B)
Demikian contoh soal dan pembahasannya tentang materi garis dan sudut. Semoga artikel ini bermanfaat. Mohon maaf jika ada kesalahan dalam postingan di atas. Salam Mafia.
Demikian contoh soal dan pembahasannya tentang materi garis dan sudut. Semoga artikel ini bermanfaat. Mohon maaf jika ada kesalahan dalam postingan di atas. Salam Mafia.







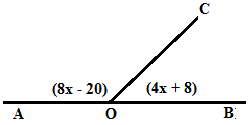

Terimakasih
BalasHapusSangat membantu
BalasHapusNo 6 nya hilang
BalasHapusTerima kasih atas perhatiannya. Sudah admin perbaiki.
Hapus