Contoh Soal Persamaan Garis Tegak Lurus Melalui Titik

Agar lebih mudah memahami contoh soal tentang persamaan garis tegak lurus melalui titik di bawah ini. Silahkan pahami terlebih dahulu materi tentang gradien dua buah garis yang tegak lurus dan menentukan persamaan garis yang melalui sebuah titik dan tegak lurus dengan sebuah garis.

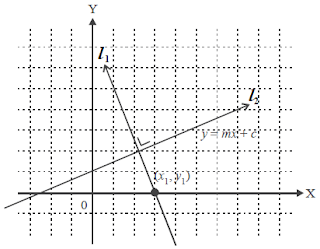Garis tegak lurus

Jika sudah pernah membaca atau sudah memahaminya, silahkan perhatikan contoh soal di bawah ini.

 

Contoh Soal 1

Tentukan persamaan garis yang melalui titik (2, 5) dan tegak lurus dengan garis 2x + y + 5 = 0

 

Penyelesaian:

Ubah persamaan garis 2x + y + 5 = 0 ke bentuk persamaan garis y = mx + c, maka:

<=> 2x + y + 5 = 0

<=> y = –2x – 5

Jadi gradien (m) persamaan garis 2x + y + 5 = 0 adalah –2.

 

Selanjutnya menentukan persamaan garis yang melalui titik (2, 5) dan tegak lurus dengan garis bergradien –2 yakni:

yakni:

<=> y – y₁ = (–1/m)(x – x₁)

<=> y – 5 = (–1/–2)(x – 2)

<=> y – 5 = ½(x – 2)

<=> (y – 5) = ½(x – 2)

Agar tidak ada bilangan pecahan maka kedua ruas dikali 2, sehingga:

<=> 2(y – 5) = x – 2

<=> 2y – 10 = x – 2

<=> 2y = x – 2 + 10

<=> 2y = x + 8

 

Contoh Soal 2

Tentukan persamaan garis melalui titik (4, 5) dan tegak lurus garis y = 2x - 3

 

Penyelesaian:

Garis y = 2x – 3 sudah dalam bentuk y = mx + c, maka gradiennya 2. Persamaan garis yang melalui titik (4, 5) dan tegak lurus dengan garis bergradien 2 yakni:

<=> y – y₁ = (–1/m)(x – x₁)

<=> y – 5 = (–1/2)(x – 4)

<=> (y – 5) = –½(x – 4)

Agar tidak ada bilangan pecahan maka kedua ruas dikali 2, sehingga:

<=> 2(y – 5) = –(x – 4)

<=> 2y – 10 = –x + 4

<=> 2y = –x + 4 + 10

<=> 2y = –x + 14

<=> 2y + x = 14

 

Contoh Soal 3

Tentukan persamaan garis melalui titik (-2, -1) dan tegak lurus garis 4x – y = – 2

 

Penyelesaian:

Ubah terlebih dahulu persamaan garis 4x – y = – 2 ke bentuk persamaan garis y = mx + c, maka:

<=> 4x – y = – 2

<=> y = 4x + 2

Jadi gradien (m) persamaan garis 4x – y = –2 adalah 4.

 

Selanjutnya menentukan persamaan garis yang tegak lurus dengan garis bergradien 4 dan melalui titik (–2, –1) yakni:

<=> y – y₁ = (–1/m)(x – x₁)

<=> y – (–1) = (–1/4)(x – (–2))

<=> (y + 1) = – ¼(x + 2)

Agar tidak ada bilangan pecahan maka kedua ruas dikali 4, sehingga:

<=> 4(y + 1) = –(x + 2)

<=> 4y + 4 = –x – 2

<=> 4y = –x – 2 – 4

<=> 4y = –x – 6

<=> 4y + x = – 6

<=> 4y + x + 6 = 0

 

Contoh Soal 4

Garis m tegak lurus garis n. Jika persamaan garis m adalah y = –½x + 1 dan garis n melalui titik (-1,-4), maka tentukan persamaan garis n.

 

Penyelesaian:

Garis y = –½x + 1 sudah dalam bentuk y = mx + c, maka gradiennya –½. Selanjutnya menentukan persamaan garis yang tegak lurus dengan garis y = –½x + 1 dan melalui titik (–1, –4) yakni:

<=> y – y₁ = (–1/m)(x – x₁)

<=> y – (–4) = (–1/–½)(x – (–1))

<=> y + 4 = 2(x + 1)

<=> y + 4 = 2x + 2

<=> y = 2x – 2

 

Contoh Soal 5

Tentukan persamaan garis yang melalui titik (-3, 2) dan tegak lurus garis yang melalui titik (5, 2) dan (-5, -3).

 

Penyelesaian:

(Untuk menjawab soal ini kamu harus paham materi cara menentukan gradien garis yang melalui dua titik). Cari terlebih dahulu gradien garis yang melalui titik (5, 2) dan (-5, -3) dengan rumus yakni:

m = (y₂ – y₁)/(x₂ – x₁)

m = (-3 – 2)/(-5 – 5)

m = -5/-10

m = ½

 

Selanjutnya menentukan persamaan garis yang tegak lurus dengan garis bergradien ½ dan melalui titik (–3, 2) yakni:

<=> y – y₁ = (–1/m)(x – x₁)

<=> y – 2 = (–1/½)(x – (–3))

<=> y – 2 = -2(x + 3)

<=> y – 2 = –2x – 6

<=> y = –2x – 4

 

Demikian artikel tentang contoh soal contoh soal persamaan garis tegak lurus melalui titik. Mohon maaf jika ada kata-kata atau hitungan yang salah dalam postingan di atas.

TOLONG DIBAGIKAN YA :