Cara Menentukan Perkalian Titik Dua Buah Vektor

Sebelumnya Mafia Online sudah mengulas tentang penjumlahan dan pengurangan dua buah vektor. Pada kesempatan ini Mafia Online akan mengulas tentang cara menentukan perkalian titik dua buah vektor. Perkalian vektor dibedakan menjadi tiga macam, yaitu perkalian vektor dengan skalar, perkalian dua buah vektor yang hasilnya berupa skalar (perkalian titik), dan perkalian dua buah vektor yang hasilnya vektor juga (perkalian silang). Untuk perkalian silang dua buah vektor akan dibahas pada postingan berikutnya.

Sebelum membahas tentang perkalian titik dua buah vektor terlebih dahulu kita akan mengulas tentang perkalian vektor dengan skalar. Perkalian vektor A dengan skalar k akan menghasilkan vektor baru kA yang besarnya k kali dari vektor A. Jika nilai k positif, maka arah vektor baru sama dengan vektor sebelumnya. Sedangkan, jika nilai k negatif maka arah vektor baru akan berlawanan arah. Bagaimana dengan perkalian titik dua buah vektor?

Sifat perkalian titik dua buah vektor ini sangat berkaitan dengan penguraian vektor. Perhatikan gambar di bawah ini.

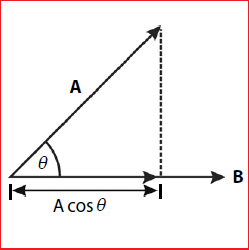
Pada gambar di atas terdapat dua buah vektor dengan membentuk sudut θ. Jika vektor A diproyeksikan terhadap vektor B maka panjang proyeksi vektor A adalah A cos θ, maka perkalian titik dari vektor A dan vektor B adalah

A • B = A cos θ . B

A • B = A B cos θ

Hasil kali titik dua buah vektor disebut juga dot product. Dua buah vektor yang dioperasikan dengan dot product menghasilkan sebuah skalar, sehingga perkalian titik dua buah vektor disebut juga sebagai perkalian skalar dua buah vektor. Untuk memantapkan pemahaman Anda tentang perkalian titik dua buah vektor, silahkan simak contoh soal di bawah ini.

Contoh Soal 1

Balok yang berada pada bidang datar licin ditarik oleh gaya 200 N dengan arah membentuk sudut 60° terhadap arah horisontal. Pada saat balok berpindah 8 m maka tentukan usaha yang dilakukan oleh gaya F.

Penyelesaian:

Usaha dapat didefinisikan sebagai perkalian titik gaya yang bekerja selama perpindahannya dengan perpindahannya. Berarti dapat diperoleh:

W = F . s

W = (F cos θ) . s

W = F s cos θ

W = 200 N . 8 m . cos 60°

W = 200 N . 8 m . ½

W = 800 Nm

W = 800 Joule (1 Nm = 1 Joule)

Masih ingatkah Anda dengan vektor satuan? Perkalian titik pada dua vektor satuan akan bernilai satu jika vektor tersebut sejenis dan akan bernilai nol jika kedua vektor tersebut tidak sejenis. Kenapa?

Sudut antara vektor satuan i dan 1 adalah 0°, maka (i)(i) cos 0° = 1, sedangkan sudut antara vektor satuan i dan j adalah 90° maka (i)(j) cos 90° = 0. Maka,

i . i = j . j = k . k = 1

i . j = i . k = j . k = 0

Secara matematis, perkalian titik vektor A dan B dapat diperoleh sebagai berikut:

A . B = (A_xi +A_yj + A_zk) . (B_xi +B_yj + B_zk)

A . B = A_xB_x +A_yB_y + A_zB_z

Contoh Soal 2

Tentukan hasil perkalian titik antara dua vektor satuan A = 3i + 4j + 6k dan B = 8i + 5j – 8k

Penyelesaian:

A . B = A_xB_x + A_yB_y + A_zB_z

A . B = 3 . 8 + 4 . 5 + 6 . (– 8)

A . B = 24 + 20 – 48

A . B = – 4

Nah demikian postingan Mafia Online tentang cara menentukan perkalian titik dua buah vektor dan contoh soal serta pembahasannya. Mohon maaf jika ada kata atau perhitungan yang salah dalam postingan ini. Salam Mafia => Kita pasti bisa.

TOLONG DIBAGIKAN YA :