Pada postingan sebelumnya, Mafia Online telah mengulas
tentang bilangan rasional. Masih ingatkah
Anda dengan pengertian bilangan rasional? Lawan dari bilangan rasional adalah bilangan irasional. Bilangan irasional adalah
bilangan yang tidak dapat dinyatakan dalam bentuk a/b dengan a, b bilangan
bulat dan b ≠ 0. Masih ingatkah Anda contoh bilangan irasional?
Contoh bilangan irasional adalah bentuk akar,
misalnya √5, √7, √11, dan √13. Pecahan bentuk akar juga termasuk bilangan
irasional, misalnya 1/√5, 3/√7, 4/√11, dan 2/√13. Penyebut yang berbentuk akar
dari pecahan tersebut dapat diubah menjadi bilangan rasional. Cara
merasionalkan setiap penyebut berlainan. Akan tetapi, prinsip dasarnya sama,
yaitu mengalikan penyebut-penyebut tersebut dengan pasangan bentuk akar
sekawannya sehingga diperoleh penyebut bilangan rasional.
Untuk lebih jelasnya, pelajari uraian berikut.
Merasionalkan
Bentuk a/√b
Cara merasionalkan bentuk a/√b adalah dengan
mengalikan pembilang dan penyebut pecahan tersebut dengan bentuk sekawan dari
penyebutnya, yaitu:
Untuk memantapkan pemahaman Anda tentang cara merasionalkan
bentuk a/√b, silahkan simak contoh soal 1 di bawah ini.
Contoh
Soal 1
Rasionalkan penyebut pecahan-pecahan berikut, kemudian
sederhanakanlah
a. 6/√2
b. 10/√5
c. 21/√3
d. 5/√5
Penyelesaian:
a. 6/√2
= (6/√2).√2/√2
=> 6/√2 = (6√2)/(√2.√2)
=> 6/√2 = (6√2)/2
=> 6/√2 = 3√2
b. 10/√5
= (10/√5).(√5/√5)
=> 10/√5 = (10√5)/(√5.√5)
=> 10/√5 = (10√5)/5
=> 10/√5 = 2√5
c. 21/√3
= (21/√3).(√3/√3)
=> 21/√3 = (21√3)/(√3.√3)
=> 21/√3 = (21√3)/3
=> 21/√3 = 7√3)
d. 5/√5
= (5/√5).(√5/√5)
=> 5/√5 = (5√5)/(√5.√5)
=> 5/√5 = (5√5)/5
=> 5/√5 = √5
Merasionalkan
Bentuk a/(b±√c)
Cara merasionalkan bentuk a/(b±√c) adalah dengan mengalikan pembilang dan
penyebut pecahan tersebut dengan bentuk sekawan dari penyebut b±√c. Bentuk
sekawan dari b + √c adalah b – √c , sedangkan bentuk sekawan dari b – √c adalah
b + √c. Berikut penjelasanya masing-masing. Untuk merasionalkan bentuk a/(b+√c),
yakni:
Untuk merasionalkan bentuk a/(b – √c), yakni:
Untuk memantapkan pemahaman Anda tentang cara merasionalkan bentuk a/(b±√c), silahkan simak contoh soal 2 di bawah ini.
Contoh
Soal 2
Rasionalkan penyebut pecahan-pecahan berikut, kemudian
sederhanakanlah
a. 4/(2 + √2)
b. 3/(3 – √5)
c. 4/(4 + √3)
d. 2/(3 – √7)
Penyelesaian:
a. 4/(2
+ √2)
= {4/(2 + √2)}.{(2 – √2)/(2 – √2)}
= {4(2 – √2)}/{2 + √2).(2 – √2)}
= (8 – 4√2)/(4 – 2)
= (8 – 4√2)/2
= 4 – 2√2
b. 2/(2
– √3) = {2/(2 – √3)}.{(2 + √3)/(2 + √3)}
= {2(2 + √3)}/{(2 – √3).(2 + √3)}
= (4 + 2√3)/(4 – 3)
= 4 + 2√3
c. 4/(2
+ √5) = {4/(2 + √5)}.{(2 – √5)/(2 – √5)}
= {4(2 – √5)}/{(2 + √5).(2 – √5)}
= 8 – 4√5)/(4 – 5)
= 8 – 4√5)/– 1
= 4√5 – 8
d. 4/(3
– √5) = {4/(3 – √5)}.{(3 + √5)/(3 + √5)}
= {4.(3
+ √5)}/{(3 + √5)(3 – √5)}
= (12 + 4√5)/(9 – 5)
= (12 + 4√5)/4
= 3 + √5
Merasionalkan
Bentuk a/(√b±√c)
Cara merasionalkan bentuk a/(√b±√c) adalah dengan mengalikan pembilang dan
penyebut pecahan tersebut dengan bentuk sekawan dari penyebut √b±√c. Bentuk
sekawan dari √b + √c adalah √b – √c , sedangkan bentuk sekawan dari √b – √c
adalah √b + √c. Berikut penjelasanya masing-masing. Untuk merasionalkan bentuk a/(√b+√c),
yakni:
Untuk merasionalkan bentuk a/(√b – √c), yakni:
Untuk merasionalkan bentuk a/(√b – √c), yakni:
Untuk memantapkan pemahaman Anda tentang cara merasionalkan bentuk a/(√b±√c), silahkan simak contoh soal 3 di bawah ini.
Contoh
Soal 3
Rasionalkan penyebut pecahan-pecahan berikut, kemudian
sederhanakanlah
a. 2/(√3 + √2)
b. 3/(√6 – √5)
c. 5/(√5 + √3)
d. 4/(√11 – √7)
Penyelesaian:
a. 2/(√3
+ √2)
= {2/(√3 + √2)}.{(√3 – √2)/(√3 – √2)}
= {2.(√3 – √2)}/{(√3 – √2).(√3 + √2)}
= (2√3 – 2√2)/(3 – 2)
= 2(√3 – √2)
b. 3/(√6 – √5)
= {3/(√6 – √5)}.{(√6 + √5)/(√6 + √5)
= {3(√6 + √5)}/{(√6 – √5)(√6 + √5)
= 3(√6 + √5)/(6 – 5)
= 3(√6 + √5)
c. 4/(√5 + √3)
= {4/(√5 + √3)}.{(√5 – √3)/(√5 – √3)}
= {4(√5 – √3)}/{(√5 + √3).(√5 – √3)}
= 4(√5 – √3)/(5 – 3)
= 4(√5 – √3)/2
= 2(√5 – √3)
d. 4/(√11 – √7)
= {4/(√11 – √7)}.{(√11 + √7)/(√11 + √7)
= {4(√11 + √7)}/{(√11 – √7)(√11 + √7)
= 4(√11 + √7)/(11 – 7)
= 4(√11 + √7)/4
= √11 + √7
Demikian postingan Mafia Online tentang cara
merasionalkan bentuk akar. Mohon maaf jika ada kata atau perhitungan yang salah
dalam postingan di atas.

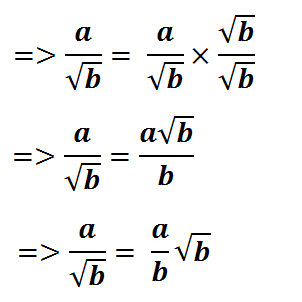




terima kasih...sangat membantu ku dalam memahami konsep soal K13...~
BalasHapusterimakasih sekali sangat membantu apalagi dengan contoh soal yg banyak dan penjelasan yg jelas terimakasih sekali
BalasHapusTerimakasih penjelasannya mudah dipahami sangat bermanfaat
BalasHapus