Rumus Dalil Proyeksi Pada Segitiga Lancip

Untuk mencari atau membuktikan dalil proyeksi pada segitiga lancip, Anda harus paham dengan pengertian proyeksi, karena untuk mencari rumus proyeksi pada segitiga lancip dapat dilakukan dengan cara memproyeksikan salah satu sisinya ke sisi yang lain. Sekarang perhatikan gambar segitiga lancip ABC di bawah ini.

Jika garis BC diproyeksikan terhadap garis AB maka garis BD merupakan hasil proyeksinya sedangkan AD merupakan sisa dari panjang sisi yang kena proyeksi, seperti gambar di bawah ini.

Masih ingatkah Anda dengan teorema Pythagoras? Sekarang perhatikan ΔACD pada Gambar 2 di atas yang siku-sikunya di D. Dengan menggunakan teorema Phytagoras maka CD dapat ditentukan dengan rumus:

CD² = AC² – AD²

t² = b² – x² . . . . (persamaan 1)

Sekarang perhatikan ΔBCD yang siku-sikunya ada di D juga. Dengan menggunakan teorema Phytagoras maka CD dapat ditentukan dengan rumus:

CD² = BC² – BD²

CD² = BC² – (AB – AD) ²

t² = a² – (c – x)²

t² = a² – (c² – 2cx + x²)

t² = a² – c² + 2cx –  x² . . . . .  (persamaan 2)

Dari persamaan (2) dan persamaan (1) akan diperoleh persamaan yang baru yakni:

a² – c² + 2cx –  x² = b² – x²

a² = b² + c² – 2cx atau

BC² = AC² + AB² – 2AB.AD

Berdasarkan penjelasan di atas maka dapat disimpulkan bahwa dalil proyeksi dapat dicari dengan cara mengkombinasikan teorema Phytagoras dengan sisa dari hasil panjang proyeksi. Misalnya jika kita mencari sisi BC, maka proyeksikan sisi BC ke salah satu sisinya misalnya sisi AB sehingga diperoleh hasil proyeksi BD. Cari panjang BC dengan teorema phytagoras (BC² = AC² + AB²) kemudian dikurangi dengan dua kali sisa hasil panjang proyeksi yang sudah dikalikan dengan panjang sisi sebagi tempat proyeksi (2AB.AD). Makaakan diperoleh panjang BC adalah:

BC² = AC² + AB² – 2AB.AD

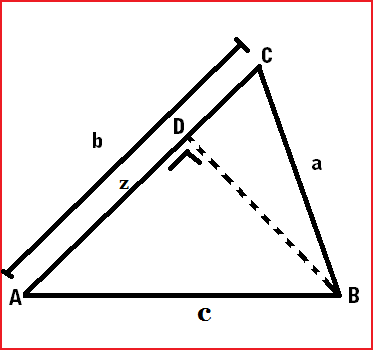
Sekarang misalkan sisi BC kita proyeksikan ke sisi AC, seperti gambar di bawah ini.

maka sisa hasil proyeksinya adalah AD. Panjnagn BC dapat dicari dengan mengkombinasikan teorema phytagoras dengan mengurangi dua kali sisa proyeksi dengan panjang sisi yang dikenai proyeksi, maka:

BC² = AC² + AB² – 2AD.AC atau

a² = b² + c² – 2bz

Latihan Soal

Sekarang perhatikan gambar di bawah ini.

Gambar di atas merupakan gambar sebuah segitiga lancip yang memproyeksikan sisi AC pada sisi AB, buktikan bahwa b² = a² + c² – 2cy.

Demikian postingan Mafia Online tentang rumus atau dalil proyeksi pada segitiga lancip. Untuk dalil proyeksi segitiga tumpul silahkan baca postingan Mafia Online berikutnya. Mohon maaf jika ada kata yang salah dalam postingan ini. Salam Mafia => Kita pasti bisa.

TOLONG DIBAGIKAN YA :