Pengertian dan Sifat-Sifat Jajargenjang

Dimanakah kamu sering melihat bangun datar berbentuk jajargenjang? Sekarang perhatikan Gambar 1 di bawah ini!

Gambar 1

Gambar 1 di atas merupakan gambar sebuah keramik atau tegel dengan motif yang unik karena semua bangun datar segi empat ada pada tegel tersebut. 

Sekarang perhatikan yang dilingkari warna merah!  Nah bangun bidang datar tersebut yang dilingkari warna merah tersebut bernama jajargenjang. Apa pengertian jajargenjang dan bagaimana sifat-sifat jajargenjang?

Pengertian jajargenjang 
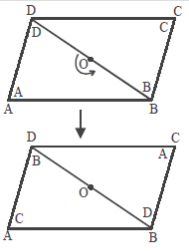
Agar Anda memahami pengertian jajargenjang, coba membuat sebarang segitiga, misalnya ΔABD. Tentukan titik tengah salah satu sisi segitiga tersebut, misalnya titik tengah sisi BD dan beri nama titik O. Kemudian, pada titik yang ditentukan (titik O) putarlah ΔABD sebesar ½ putaran (180°), sehingga terbentuk bangun ABCD seperti Gambar 2 di bawah ini.

Gambar 2

Bangun segitiga BCD merupakan bayangan dari segitiga ABD. Bangun segitiga dan bayangannya yang terbentuk itulah yang dinamakan bangun jajargenjang. Jadi pengertian jajargenjang adalah bangun segi empat yang dibentuk dari sebuah segitiga dan bayangannya yang diputar setengah putaran (180°) pada titik tengah salah satu sisinya.

Sifat-Sifat Jajargenjang 
Sekarang perhatikan Gambar 3 di bawah ini.

Gambar 3

Pada Gambar 3 menunjukkan jajargenjang ABCD. Putarlah ΔABD setengah putaran (180°) pada titik O, sehingga diperoleh AB <---> DC dan AD <---> BC. Akibatnya, AB = DC dan AD = BC. Pada setiap jajargenjang sisi-sisi yang berhadapan sama panjang dan sejajar. 

Pada Gambar 3 di atas, perhatikan sudut-sudutnya. Jika jajargenjang diputar setengah putaran (180°) maka diperoleh ∠A menjadi ∠C, ∠ABD <---> ∠BDC, dan ∠ADB <---> ∠CBD. Akibatnya ∠A = ∠C, ∠ABD = ∠BDC, dan ∠ADB = ∠CBD, sedemikian sehingga ∠A = ∠C, ∠B = ∠ABD + ∠CBD, dan ∠D = ∠ADB + ∠BDC. Pada setiap jajargenjang sudut-sudut yang berhadapan sama besar. 

Selanjutnya, perhatikan 4 di bawah ini! 

Gambar 4

Pada jajargenjang ABCD tersebut AB // DC dan AD // BC. Ingat kembali materi terdahulu mengenai garis dan sudut. Berdasarkan sifat-sifat garis sejajar, karena AB // DC, maka diperoleh

• sudut A dalam sepihak dengan sudut D, maka sudut A + sudut D = 180°.
• sudut B dalam sepihak dengan sudut C, maka sudut B + sudut C = 180°.

Demikian juga karena AD // BC, maka diperoleh

• sudut A dalam sepihak dengan sudut B, maka sudut A + sudut B = 180°.
• sudut D dalam sepihak dengan sudut C, maka sudut C + sudut D = 180°.

Hal tersebut dapat dituliskan sebagai berikut.

• sudut A + sudut D = sudut A + sudut B = 180°
• sudut C + sudut B = sudut C + sudut D = 180°

Dari uraian di atas, dapat disimpulkan sebagai berikut. Pada setiap jajargenjang jumlah pasangan sudut yang saling berdekatan adalah 180°.  

 

Sekarang, perhatikan Gambar 5 berikut ini. 

Gambar 5

Pada gambar di atas, jika ΔABD diputar setengah putaran (180°) pada titik O, akan diperoleh OA <---> OC dan OB <---> OD. Hal ini menunjukkan bahwa OA = OC dan OB = OD. Padahal OA + OC = AC dan OB + OD = BD. Jadi, dapat disimpulkan bahwa pada setiap jajargenjang kedua diagonalnya saling membagi dua sama panjang. 

Berdasarkan uraian di atas, dapat ditarik kesimpulan bahwa sifat-sifat jajargenjang sebagai berikut.

1. Sisi-sisi yang berhadapan pada setiap jajargenjang sama panjang dan sejajar.
2. Sudut-sudut yang berhadapan pada setiap jajargenjang sama besar.
3. Jumlah pasangan sudut yang saling berdekatan pada setiap jajargenjang adalah 180°.
4. Pada setiap jajargenjang kedua diagonalnya saling membagi dua sama panjang.

Untuk memantapkan pemahaman kamu mengenai sifat-sifat jajargenjang, perhatikan contoh soal berikut.

Contoh Soal
Perhatikan Gambar 6 di bawah ini.

Gambar 6

Pada jajargenjang KLMN di atas, diagonal-diagonalnya berpotongan di titik P. Jika diketahui panjang KL = 10 cm, LM = 8 cm, dan ∠KLM = 112°, tentukan (a) panjang MN; (b) panjang KN; (c) besar ∠KNM; dan (d) besar ∠LKN.

Penyelesaian:
KL = 10 cm

LM = 8 cm

∠KLM = 112°.

(a) Dengan menggunakan sifat-sifat jajargenjang bahwa sisi-sisi yang berhadapan pada setiap jajargenjang sama panjang dan sejajar, maka:
MN = KL = 10 cm 

(b) Hampir sama caranya seperti bagian (a), dengan menggunakan sifat-sifat jajar genjang maka: 
KN = LM = 8 cm 

(c) Sifat-sifat jajargenjang bahwa sudut-sudut yang berhadapan pada setiap jajargenjang sama besar, maka:
∠KNM = ∠KLM (sudut yang berhadapan) = 112° 

(d) Jumlah pasangan sudut yang saling berdekatan pada setiap jajargenjang adalah 180°, maka:
∠LKN  + ∠KNM = 180° (sudut yang berdekatan) 
∠LKN + 112° = 180° 
∠LKN = 180° – 112° = 68°

Untuk contoh soal yang lain tunggu update postingan Mafia Online. Demikian  pembahasan mengenai pengertian dan sifat-sifat jajargenjang. Untuk mencari keliling dan luas jajargenjang, silahkan baca postingan mafia online tentang keliling dan luas jajargenjang.

TOLONG DIBAGIKAN YA :