Untuk gerak benda dalam satu bidang, kecepatan didefinisikan sebagai
perubahan posisi dalam interval waktu tertentu. Oleh karena kecepatan dan
percepatan merupakan besaran vektor, maka fungsi kecepatan dapat diperoleh
dari fungsi percepatan dengan metode integral, yaitu:
a = dv/dt
dv = a dt
ꭍdv = ꭍa dt
dengan mengintegralkan kedua ruas, di mana batas atas
integral dv yakni vt dan batas bawah integral dv yakni v0.
Sedangkan batas atas intagral a dt
yakni t dan batas bawah integral yakni 0, maka:
vt – v0 = ꭍa dt
vt = v0 + ꭍa dt
keterangan:
vt = kecepatan benda saat t sekon (m/s)
v0 = kecepatan awal benda saat t = 0 (m/s)
a = percepatan
benda (m/s2)
Apabila vektornya disesuaikan menurut arah sumbu-x dan
sumbu-y, maka persamaan tersebut berubah menjadi:
vt = (v0y + ꭍaX dt)i + (v0y + ꭍay dt)j
Secara matematis, integral adalah penjumlahan yang
kontinu. Metode yang digunakan untuk memeroleh nilai kecepatan dari fungsi
percepatan dapat dilakukan dengan analogi pada cara untuk mendapatkan nilai
perpindahan dari fungsi kecepatan. Grafik besar percepatan terhadap waktu dari
gerak suatu benda dapat dilihat seperti gambar di bawah ini.
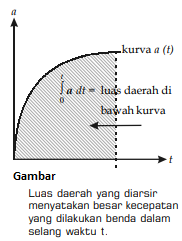
Luas daerah yang diarsir, yaitu luas daerah yang dibatasi
oleh grafik besar percepatan sebagai fungsi waktu a(t) dengan sumbu horizontal t adalah perubahan kecepatan gerak
benda. Kecepatan partikel secara grafik dapat ditentukan sebagai berikut.
Besar kecepatan = luas daerah di bawah kurva a (t)
Untuk memantapkan pemahaman kamu tentang materi
menentukan kecepatan dari fungsi percepatan, silahkan simak contoh soal di
bawah ini.
Contoh
Soal 1
Sebuah benda bergerak dengan kecepatan awal 3 m/s. Jika
benda mengalami percepatan a (t) = (4t –2) m/s2, tentukanlah persamaan
kecepatan benda dan hitung kecepatan benda pada t = 2 sekon
Penyelesaian:
Diketahui:
Vo = 3 m/s
a(t) = (4t – 2) m/s2
Kecepatan dapat diperoleh dari fungsi percepatan dengan
metode integral.
v = v0
+ ∫ a dt = 3 + ∫
(4t – 2) dt = (3 + 2t2 – 2 t) m/s2
.
b. Kecepatan benda pada saat t = 2 sekon adalah
v = 3 + (2)(2)2
– (2)(2) = 7 m/s.
Contoh
Soal 2
Benda bergerak dengan kecepatan awal 3 m/s. Jika benda
mengalami percepatan a(t) = (4t – 2) m/s2, tentukanlah persamaan kecepatan
benda dan kecepatan benda pada t = 2 sekon.
Contoh
Soal 3
Sebuah partikel bergerak lurus dengan percepatan a = (2 –
3t2) m/s2. Jika
kecepatan dan perpindahan partikel pada waktu t = 1 sekon
adalah v1 = 3
m/s dan S1 = 3⁄
4 m. Tentukan kecepatan dan perpindahan partikel sebagai
fungsi waktu
Soal
Latihan
Mobil Andra mula-mula diam, kemudian selama 4 s
dipercepat dengan percepatan a = 2t i + 3t2 j.
Tentukan:
a. vektor kecepatannya,
b. komponen sumbu X dan Y vektor kecepatannya,
c. besar kecepatan mobil Andra saat t = 2 s.
0 Response to "Menentukan Kecepatan Dari Fungsi Percepatan"
Posting Komentar
Terima kasih sudah membaca blog ini, silahkan tinggalkan komentar dengan sopan dan tidak mengandung unsur SARA atau pornografi serta tidak ada link aktif. Mohon maaf kalau komentarnya dibalas agak lambat. Kolom komentar ini kami moderasi, jadi kalau ada komentar yang tidak sesuai dengan ketentuan tidak akan dipublikasikan.