Untuk menjawab soal kombinasi antara persegi dan
lingkaran, kamu harus paham terlebih dahulu tentang materi persegi dan
lingkaran, khususnya tentang luas. Oke, jika kamu sudah paham kedua konsep
tersebut, silahkan simak contoh soal di bawah ini.
Contoh
Soal
Perhatikan gambar di bawah ini!

Hitunglah luas daerah yang diarsir dan tidak diarsir di
bawah ini.
Penyelesaian:
Untuk menyelesaian soal di atas terlebih dahulu harus
mencari daerah yang diarsir dengan menggunakan konsep luas juring ¼ lingkaran.
Di sini ada 4 juring yakni 1 juring dengan jari-jari 14 cm dan 3 juring dengan
jari-jari 7 cm.
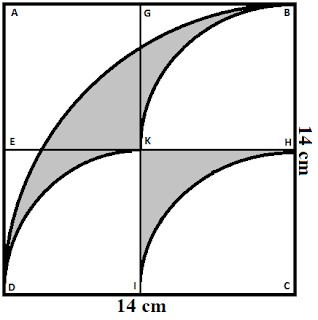
Untuk mencari luas yang diarsir dengan cara luas juring
dengan jari-jari 14 cm dikurangi dengan 3 juring dengan jari-jari 7 cm. Dengan
menggunakan cara cepat menghitung luas juring maka:
Luas juring AB = ¼ πr2
Luas juring AB = ¼ (22/7)(14 cm)2
Luas juring AB
= 154 cm2
Luas Juring BK = ¼ πr2
Luas Juring BK = ¼ (22/7)(7 cm)2
Luas juring BK
= 38,5 cm2
Dalam hal ini luas juring BK = luas juring DK = luas
juring IH, maka:
Luas arsiran = Luas Juring AB – 3 luas juring BK
Luas arsiran = 154 cm2 – 3.(38,5 cm2)
Luas arsiran = 115,5 cm2
Sekarang hitung luas persegi ABCD yakni:
Luas persegi ABCD = sisi x sisi
Luas persegi ABCD = 14 cm x 14 cm
Luas persegi ABCD = 196 cm2
Sedangkan untuk menghitung luas yang tidak diarsir dapat
dilakukan dengan cara mengurangkan luas persegi dengan luas daerah yang
diarsir, maka:
Luas tidak diarsir = luas persegi ABCD – luas arsiran
Luas tidak diarsir = 196 cm2 – 115,5 cm2
Luas tidak diarsir = 80,5 cm2
Jadi luas daerah yang tidak diarsir pada gambar tersebut
adalah 80,5 cm2.
0 Response to "Contoh Soal dan Pembahasan Kombinasi Antara Persegi dan Lingkaran"
Posting Komentar
Terima kasih sudah membaca blog ini, silahkan tinggalkan komentar dengan sopan dan tidak mengandung unsur SARA atau pornografi serta tidak ada link aktif. Mohon maaf kalau komentarnya dibalas agak lambat. Kolom komentar ini kami moderasi, jadi kalau ada komentar yang tidak sesuai dengan ketentuan tidak akan dipublikasikan.