Agar
lebih mudah memahami contoh soal di bawah ini, alangkah baiknya jika anda sudah
memahami cara menghitung jarak dari titik ke suatu bidang pada kubus (silahkan
baca: cara menghitung jarak titik ke titik, garis, dan bidang). Jika sudah
paham dengan materinya, silahkan simak dan pahami contoh soal di bawah ini.
Contoh Soal 1
Diketahui
kubus ABCD.EFGH dengan panjang rusuk 12 cm. Tentukan jarak titik C ke bidang
BDG.
Penyelesaian:
Untuk
memudahkan menyelesaikan soal ini kita gambar dulu bentuk kubusnya, seperti
gambar di bawah ini.
P
merupakan titik perpotongan antara diagonal AC dan BD maka,
Panjang AC
yakni:
AC = s√2
AC = 12√2
cm
Panjang
PC yakni:
PC = ½AC
= 6√2 cm
Panjang
PG (dengan teorema Pythagoras) yakni:
PG2
= PC2 + CG2
PG2
= (6√2)2 + 122
PG2
= 72 + 144
PG = √216
PG = 6√6
cm
Dengan
menggunakan kesebangunan segitiga maka ΔCPX sebagun dengan ΔPCG, maka:
PC/PG =
CX/CG
6√2/6√6 =
CX/12
√2/√6 =
CX/12
CX = 12√2/√6
CX = 12/√3
CX = 4√3
cm
Contoh Soal 2
Diketahui
kubus ABCD.EFGH dengan panjang rusuk 6 cm. Tentukan jarak titik C ke bidang AFH.
Penyelesaian:
Kita
gambar dulu bentuk kubusnya, maka akan tampak seperti gambar di bawah ini:
P
merupakan titik perpotongan antara diagonal EG dan FH dan CX merupakan jarak
antara bidang AFH dengan titik C, maka,
Panjang AC
yakni:
AC = s√2
AC = 6√2
cm
Panjang
EP yakni:
EP = ½AC
= 3√2 cm
Panjang CP
= AP yakni:
AP2
= AE2 + EP2
AP2
= 62 + (3√2)2
AP = √54
AP = 3√6
cm
Perhatikan
ΔACP, merupakan segitiga sama kaki dengan tinggi sama dengan panjang rusuk
kubus. Dengan menggunakan perbandingan luas segitiga maka:
L.ΔACP = L.ΔACP
½ AC.AE =
½ AP.CX
CX =
AC.AE/AP
CX = 6√2
. 6/3√6
CX = 12/√3
CX = 4√3
cm
Nah
demikian contoh soal dan pembahasan cara menghitung jarak dari titik ke suatu bidang
pada bangun ruang kubus, jika ada permasalahan atau kendala dalam memahami contoh
soal ini, silahkan tanyakan pada kolom komentar. Kita pasti bisa.
Update**
Contoh soal di ambil dari komentar
Sebuah kubus ABCD.EFGH dengan
panjang rusuk 6 cm. Titik P ditengah AE dan titik Q ditengah AF. Berapakah
jarak garis EF dengan bidang PQGH. Mohon solusi!
Penyelesaian:
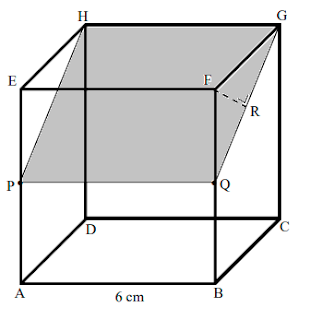
Jika digambarkan akan tampak seperti
gambar di bawah ini
 |
| Gambar ilustrasi |
Jarak garis EF dengan bidang PQGH
sama dengan panjang garis FR. Untuk mencari garis FR kita gunakan konsep
kesebangunan pada bangun datar. Perhatikan segitiga siku-siku QFG yang titik
siku-sikunya berada di titik F. Dengan panjang FG = 6 cm dan panjang FQ = ½ BF
= 3 cm
Panjang GQ dapat dicari dengan
menggunakan teorema Phytagoras yakni:
GQ2 = FQ2 + FG2
GQ2 = 32 + 62
GQ2 = 9 + 36
GQ2 = 45
GQ = √45
GQ = √9. √5
GQ = 3√5
Dengan menggunakan konsep kesetaraan
atau kesembangunan luas segitiga maka:
L∆ = L∆
½ FQ.FG = ½ GQ.FR
FQ.FG = GQ.FR
3 . 6 = 3√5 . FR
6 = √5 . FR
FR = 6/√5
FR = (6/5)√5
Jadi, jarak garis EF dengan bidang PQGH
adalah 6/√5 atau (6/5)√5. Semoga membantu.



Terima kasih atas pembahasannya
BalasHapusterima kasih atas soal dan pembahasannya, sangat membantu dalam belajar
BalasHapussebuah kubus ABCDEFGH dengan panjang rusuk 6 cm.titik P ditengah AE dan titik Q ditengah AF.berapakah jarak garis EF dengan bidang PQGH. mohon solusi
BalasHapusSudah admin tambahkan solusinya lengkap dengan gambarnya pada postingan ini, silahkan disimak dan dipahami ya. Jika ada kendala dalam memahami solusi tersebut silahkan tanyakan lagi. Mohon maaf jika Admin lambat membalas komentarnya karena ada kegiatan yang sangat mendesak. Mohon maaf juga jika ada kekeliruan dalam memberikan solusi. Terima kasih sudah berkunjung ke blog ini.
Hapus