Agar lebih mudah memahami contoh soal di bawah
ini, alangkah baiknya jika anda sudah memahami cara menghitung besar sudut yang
dibentuk oleh garis dan bidang yang sudah dibahas pada postingan sebelumnya
(silahkan baca: cara mencari besar sudut antara garis dan bidang). Jika sudah paham dengan materinya, silahkan simak
dan pahami contoh soal di bawah ini.
Contoh
Soal 1
Sebuah kubus ABCD.EFGH memiliki panjang rusuk 12
cm dan titik P ditengah-tengah AD. Tentukan nilai sin α, jika α adalah sudut
yang dibentuk oleh garis HP dengan bidang BDHF.
Penyelesaian:
Untuk memudahkan menyelesaikannya kita gambar
dulu bentuk kubusnya, yakni seperti gambar di bawah ini.

Jika garis HP diproyeksikan terhadap bidang BDHF
akan terbentuk garis HR dengan PR = QR. Sekarang kita hanya mencari panjang
garis PR dan HP dengan menggunakan teorema Pythagoras yakni:
PQ2 = DP2 + DQ2
PQ2 = 62 + 62
PQ = √72 = 6√2 cm
maka:
PR = ½ PQ = 3√2 cm
HP2 = DP + DH2
HP2 = 62 + 122
HP2 = 36 + 144
HP = √180 = 6√5 cm
sin α = PR/HP
sin α = 3√2/6√5
sin α = (3/30)√10
sin α = (1/10)√10
Contoh
Soal 2
Diketahui sebuah kubus ABCD.EFGH memiliki
panjang rusuk 4 cm. Jika titik P merupakan berada di tengah-tengah garis AE dan
α merupakan sudut yang dibentuk oleh bidang FHP dengan bidang AFH, tentukan
nilai sin α.
Penyelesaian:
Untuk memudahkan menyelesaikannya kita gambar
dulu bentuk kubusnya, yakni seperti gambar di bawah ini.
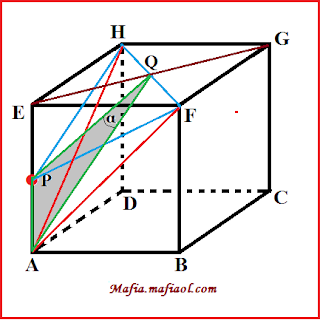
α merupakan sudut yang dibentuk oleh garis PQ
dengan AQ, oleh karena itu kita harus mencari panjang AP, AQ, dan PQ. Panjang
AP merupakan setengah panjang rusuk kubus yakni:
AP = ½ AE = 2 cm
EG merupakan panjang diagonal bidang kubus.
Dapat dicari dengan rumus:
d = s√2
EG = AB√2
EG = 4√2 cm
maka:
EQ = ½ EG = 2√2 cm
Panjang AQ dapat dicari dengan teorema
Pythagoras yakni:
AQ2 = AE2 + EQ2
AQ2 = 42 + (2√2)2
AQ2 = 16 + 8
AQ = √24 = 2√6 cm
Panjang PQ juga dapat dicari dengan teorema
Pythagoras yakni:
PQ2 = EP2 + EQ2
PQ2 = 22 + (2√2)2
PQ2 = 4 + 8
PQ = √12 = 2√3 cm
Untuk mencari sin α kita harus mencari nilai cos
α dengan menggunakan aturan cosinus yakni:
AP2 = PQ2 + AQ2
– 2.PQ.AQ.cos α
22 = (2√3)2 + (2√6)2
– 2.2√3.2√6.cos α
4 = 12 + 24 – 24√2.cos α
–32 = – 24√2.cos α
cos α = 32/(24√2)
cos α = (32/48)√2
cos α = (2/3)√2
Dengan menggunakan identitas trigonometri maka
nilai sin α dapat dicari yakni:
sin2 α + cos2 α = 1
sin2 α = 1 – cos2 α
sin2 α = 1 – [(2/3)√2]2
sin2 α = 1 – 8/9
sin2 α = 1/9
sin α = (1/9)
sin α = 1/3
Nah demikian contoh soal serta pembahannya
tentang cara mencari besar atau nilai sutau sudut yang dibentuk oleh garis dengan
bidang pada bangun ruang kubus. Jika ada permasalahan atau kendala dalam
memahami contoh soal ini, silahkan tanyakan pada kolom kometar. Kita pasti
bisa.
Terima kasih segala ilmunya, semoga mendapat balasan dari Alloh SWT
BalasHapus