Agar
lebih mudah memahami contoh soal di bawah ini, alangkah baiknya jika anda sudah
memahami cara menghitung jarak titik ke titik pada kubus (silahkan baca: cara menghitung jarak titik ke titik, garis, dan bidang). Jika sudah paham dengan
materinya, silahkan simak dan pahami contoh soal di bawah ini.
Contoh Soal 1
Diketahui
kubus ABCD.EFGH dengan panjang rusuk 10 cm. Tentukan jarak titik A ke C dan
titik A ke G.
Penyelesaian:
Untuk
memudahkan menyelesaikan soal ini kita gambar dulu bentuk kubusnya, seperti
gambar di bawah ini.
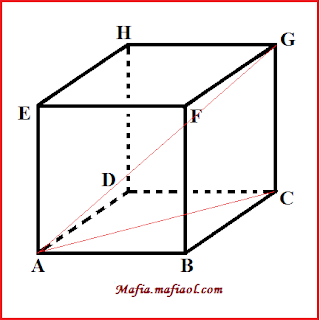
Jarak dari
titik A ke C merupakan panjang diagonal
bidang atau sisi pada kubus ABCD.EFGH, panjang diagonal sisi atau bidang
dapat dicari dengan dua cara yakni dengan menggunakan teorema pythagoras dan
dengan rumus. Untuk menggunakan teorema Pythagoras yakni:
AC2
= AB2 + BC2
AC2
= 102 + 102
AC2
= 200
AC = √200
AC = 10√2
cm
Sedangkan
untuk dengan rumus dapat menggunakan rumus:
d = s√2
d = 10√2
cm
Jadi
jarak titik A ke C yakni 10√2 cm
Jarak
titik A ke G merupakan panjang diagonal ruang kubus. Panjang diagonal ruang
pada kubus dapat dicari dengan teorema Pythagoras dan dengan rumus. Untuk cara
teorema Pythagoras yakni:
AG2
= AC2 + CG2
AG2
= (10√2)2 + 102
AG2
= 200 + 100
AG = √300
AG = 10√3
cm
Sedangkan
untuk dengan rumus dapat menggunakan rumus:
d = s√3
d = 10√3
cm
Jadi
jarak titik A ke G yakni 10√3 cm
Contoh Soal 2
Diketahui
kubus ABCD.EFGH dengan panjang rusuk 12 cm. Titik P terletak di tengah garis AE.
Tentukan jarak titik P ke B dan titik P ke C.
Penyelesaian:
Kita
gambar dulu bentuk kubusnya, maka akan tampak seperti gambar di bawah ini:

Perhatikan
segitiga siku-siku ABP pada sisi ABFE, panjang AP = ½ AE = 6 cm, maka:
PB2
= AB2 + AP2
PB2
= 122 + 62
PB2
= 144 + 36
PB2
= 180
PB = √180
PB = 6√5
cm
Jadi, jarak
titik P ke B adalah 6√5 cm
Perhatikan
segitiga siku-siku ACP, panjang AC merupakan diagonal sisi kubus yakni:
d = s√2
d = 12√2
cm
dengan
menggunakan teorema Pythagoras maka panjang PC yakni:
PC2
= AC2 + AP2
PC2
= (12√2)2 + 62
PC2
= 288 + 36
PC2
= 324
PC = √324
PC = 18
cm
Jadi, jarak
titik P ke C adalah 18 cm
Nah
demikian contoh soal dan pembahasan cara menghitung jarak titik ke titik pada bangun
ruang kubus, jika ada permasalahan atau kendala dalam memahami contoh soal ini,
silahkan tanyakan pada kolom komentar. Kita pasti bisa.
Min kenapa menanyakan PC menggunakan teorema Phytagoras itu ditambah +,sisi miringnya itu PC atau AC ya min?
BalasHapusUntuk segitiga ABC sisi miringnya AC, sedangkan untuk segitiga ACP sisi miringnya PC.
Hapusitu yg nomer 1..soalnya titik B ke C,,tp penjelasan dan hasilnya kok A ke C?
BalasHapusSebenarnya soalnya bukan titik B ke C tetapi A ke C. titik B ke C merupakan panjang rusuk kubus. Mohon maaf atas kesalahan ketik ini. Soalnya sudah saya perbaiki. Terima kasih atas koreksi dan kunjungannya 🙏
Hapus