Besar dan Arah Resultan Vektor Saling Tegak Lurus

Postingan tentang besar dan arah resultan vektor saling tegak lurus ini merupakan lanjutan dari postingan sebelumnya tentang besar dan arah resultan vektor yang segaris dan juga penjabaran dari cara menentukan besar dan arah resultan dua buah vektor. Untuk lebih memudahkan Anda memahami resultan vektor yang tegak lurus, Anda harus tahu yang mana suatu vektor dikatakan tegak lurus terhadap vektor lainnya.

Contoh dalam kehidupan sehari-hari yang berkaitan dengan vektor yang saling tegak lurus yaitu orang yang menyeberangi sungai dengan menggunakan sampan.

Gambar 1
Sumber gambar: Wikipedia

Sampan tersebut akan menuju ke seberang tepi sungai dengan kecepatan tertentu, tetapi dari arah yang tegak lurus dengan sampan ada arus air sungai yang bergerak dengan kecepatan tertentu juga. Jika digambarkan skemanya seperti Gambar 2 di bawah ini.

Gambar 2

Dari bagan Gambar 2 di atas terlihat bahwa sampan dari titik A akan bergerak ke titik B dengan kecepatan v_s, akan tetapi pada arah yang tegak lurus mengalir arus air sungai dengan kecepatan v_a. Apakah sampan akan tepat sampai di titik B?

Tentu jawabannya tidak, karena perahu tersebut akan bergerak dengan keadaan miring dengan sudut tertentu. Resultan ini dapat digambarkan secara grafis seperti pada Gambar 3 seperti gambar di bawah ini.

Gambar 3

Dari gambar 3 di atas terlihat bahwa resultan kecepatan sampan (v_s) terhadap arus air sungai (v_a) adalah (v_R). Jadi, sampan tersebut tidak tepat akan sampai di titik B melainkan di titik C. Ternyata dua vektor yang saling tegak lurus maka resultannya dapat membentuk segitiga siku-siku. Bagaimana menentukan besar resultan dua buah vektor yang tegak lurus?

Untuk menentukan besar dua buah vektor yang saling tegak lurus dapat kita gunakan rumus menentukan besar dua buah vektor yakni:

(v_R)² = (v_a)² + (v_s)² + 2v_a.v_s.cos α

Karena arah vektornya tegak lurus maka sudut yang dibentuk oleh dua vektor tersebut adalah 90°. Ingat cos 90 = 0, maka rumusnya menjadi:

(v_R)² = (v_a)² + (v_s)² + 2v_a.v_s.0

(v_R)² = (v_a)² + (v_s)²

Jadi, besarnya resultan dua vektor yang saling tegak lurus yakni:

v_R² = v_a² + v_s²

Ternyata rumus tersebut memenuhi dalil Pythagoras, hal ini karena resultan dari vektor-vektor tersebut menghasilkan bentuk segitiga siku-siku. Bagaimana menentukan arah resultan dari kedua vektor tersebut?

Untuk menentukan arah resultan dua buah vektor yang saling tegak lurus perhatikan gambar 4 berikut ini.

Gambar 4

Dari gambar 4 di atas terlihat bahwa sudut yang dibentuk oleh dua buah vektor yang saling tegak lurus adalah sudut α. Untuk mencari nilai dari sudut α dapat menggunakan rumus tangen yakni:

Tan α = v_s/v_a

dan

α = arc tan (v_s/v_a)

dengan :

v_s ,v_a = besar dua vektor yang saling tegak lurus

v_R = besar resultan vektor

α = sudut resultan vektor terhadap vektor v_a.

Untuk memantapkan pemahaman Anda tentang vektor yang arahnya saling tegak lurus silahkan simak contoh soal di bawah ini.

Contoh Soal

Cekok akan menyeberangi sebuah sungai dengan menggunakan sampan. Jika sampan yang ia kayuh dapat menghasilkan kecepatan 2 m/s, sedangkan arus air di sungai itu memiliki kecapatan 5 m/s. Tentukan besar dan arah resultan dari sampan tersebut.

Penyelesaian:

 Jika kita misalkan kecepatan sampan = v_s dan kecepatan arus air = v_a, maka soal tersebut dapat dinyatakan ke dalam gambar seperti berikut di bawah ini.

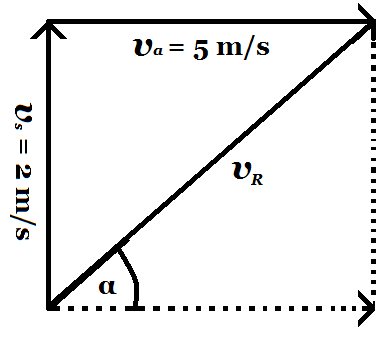Gambar 5

maka:

v_R² = v_a² + v_s²

v_R² = 5² + 2²

v_R² = 25 + 4

v_R² = 29

v_R = √29

v_R = 5,4

Jadi besar resultan dari kecepatan perahu tersebut adalah 5,4 m/s

α = arc tan (v_s/v_a)

α = arc tan (2/5)

α = arc tan 0,4

α = 21.8°

Jadi arah resultan dari kecepatan perahu tersebut adalah 21.8° terhadap sisi sungai.

Demikian postingan Mafia Online tentang besar dan arah resultan vektor yang tegak lurus dan contoh soalnya. Mohon maaf jika ada kata atau perhitungan yang salah dalam postingan ini. Salam Mafia => Kita pasti bisa.

TOLONG DIBAGIKAN YA :