Masih ingatkah Anda dengan operasi pembagian pada bilangan bulat? Kita ketahui bahwa operasi
pembagian pada bilangan bulat merupakan invers (kebalikan) dari perkalian. Hal
ini juga berlaku pada pembagian bilangan
pecahan.
Pembagian
Pecahan oleh Bilangan Bulat
Untuk lebih mudah memahami operasi pembagian
pecahan oleh bilangan bulat, silahkan simak contoh soal berikut ini. “Yanti memiliki 2/3 meter pita yang akan
digunakan untuk mengikat rambutnya, kemudian dia membaginya menjadi dua bagian
yang sama. Dapatkah kamu tentukan berapa panjang tiap bagian pita tersebut”.
Untuk menyelesaiakan permasalahan itu, silahkan perhatikan
gambar di bawah ini.

Dari ilustrasi di atas dapat terlihat bahwa jika
2/3 meter dibagi menjadi dua bagian, maka masing-masing pita akan memiliki panjang
1/3 meter. Sehingga (2/3) : 2 = 1/3. Oleh karena itu dapat disimpulkan bahwa
jika a/b merupakan bilangan pecahan dan dengan c merupakan bilangan bulat,
maka:
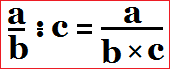
Contoh
Soal 1
Tentukan hasil pembagian dari bilangan pecahan
dengan bilangan bulat berikut ini.
a. ½ : 7
b. (2/3) : 6
c. ¾ : 6
d. (3/5) : 5
Penyelesaian:
a. ½ : 7 = 1/(2×7) = 1/14
b. (2/3) : 6 = 2/(3×6) = 2/18 = 1/9
c. ¾ : 6 = 3/(4×6) = 3/24 = 1/8
d. (3/5) : 5 = 3/(5×5) = 3/25
Pembagian
Pecahan oleh Bilangan Pecahan dengan Penyebut Sama
Untuk lebih mudah memahami operasi pembagian
pecahan oleh bilangan pecahan dengan penyebut sama, silahkan simak contoh soal
berikut ini. “Ida memiliki 8/9 meter pita
yang akan digunakan untuk mengikat rambutnya, kemudian ia memotong pita
tersebut masing-masing menjadi 2/9 meter. Dapatkah kamu tentukan berapa banyak
potongan pita tersebut”.
Untuk menyelesaiakan permasalahan itu, silahkan perhatikan
gambar di bawah ini.

Dari ilustrasi di atas dapat terlihat bahwa jika
8/9 meter pita dibagi dengan 2/9 meteran, maka akan terdapat empat bagian pita
dengan panjang masing-masing 2/9 meter. Sehingga (8/9) : (2/9) = 4. Oleh karena
itu dapat disimpulkan bahwa jika a/c dan b/c merupakan bilangan pecahan, maka:

Contoh
Soal 2
Tentukan hasil pembagian dari bilangan pecahan
dengan bilangan bulat berikut ini.
a. (8/7) : (5/7)
b. (2/3) : (4/3)
c. ¾ : ¼
d. (3/5) : (2/5)
Penyelesaian:
a. (8/7) : (5/7) = 8/5
b. (2/3) : (4/3) = 2/4 = ½
c. ¾ : ¼ = 3/1 = 3
d. (3/5) : (2/5) = 3/2 = 1½
Pembagian
Bilangan Bulat oleh Bilangan Pecahan
Untuk lebih mudah memahami operasi pembagian bilangan
bulat oleh bilangan pecahan, silahkan simak contoh soal berikut ini. “Untuk menguji kandungan suatu zat, terlebih
dahulu Benot memasukan zat tersebut ke dalam air. Benot memiliki segelas air, kemudian
Benot membagi air itu menjadi beberapa gelas dengan masing-masing berisi ¼ bagian
gelas. Ada berapa zat yang akan diuji Benot”.
Untuk menyelesaiakan permasalahan itu, silahkan perhatikan
gambar di bawah ini.

Dari ilustrasi di atas dapat terlihat bahwa jika
segelas air dibagi dengan ¼ an gelas, maka akan terdapat empat bagian gelas
dengan ukuran isi ¼ gelas air. Sehingga 1 : ¼ = 4. Oleh karena itu dapat
disimpulkan bahwa jika a merupakan bilangan bulat dan b/c merupakan bilangan
pecahan, maka:

Contoh
Soal 3
Tentukan hasil pembagian dari bilangan bulat
dengan bilangan pecahan berikut ini.
a. 2 : (5/7)
b. 3 : (11/3)
c. 1 : ½
d. 6 : (19/3)
Penyelesaian:
a. 2 : (5/7) = (2×7)/5 = 14/5
b. 3 : (11/3) = (3×3)/11 = 9/11
c. 1 : ½ = (1×2)/1 = 2/1 = 2
d. 6 : (19/3) = (6×3)/19 = 18/19
Pembagian
Pecahan oleh Bilangan Pecahan dengan Penyebut Berbeda
Untuk lebih mudah memahami operasi pembagian
pecahan oleh bilangan pecahan dengan penyebut berbeda, silahkan simak contoh
soal berikut ini. “Cekok memiliki 3/4
meter kayu, kemudian ia memotong kayu tersebut menjadi beberapa bagian dengan
panjang masing-masing potongan kayu menjadi 1/8 meter. Dapatkah kamu tentukan
berapa banyak potongan kayu tersebut”.
Untuk menyelesaiakan permasalahan itu, silahkan perhatikan
gambar di bawah ini.

Dari ilustrasi di atas dapat terlihat bahwa jika
¾ meter kayu kemudian dipotong-potong dengan ukuran yang sama dengan ukuran
masing-masing potongan adalah 1/8 meter, maka akan terdapat enam bagian potongan
kayu dengan panjang masing-masing 1/8 meter. Sehingga (3/4) : (1/8) = 6. Oleh
karena itu dapat disimpulkan bahwa jika a/b dan c/d merupakan bilangan pecahan,
maka:

Contoh
Soal 4
Tentukan hasil pembagian dari bilangan pecahan
dengan bilangan pecahan dengan penyebut berbeda berikut ini.
a. (8/7) : (5/9)
b. (2/3) : (4/5)
c. ¾ : ½
d. (3/5) : (2/3)
Penyelesaian:
a. (8/7) : (5/9)
= (8/7) × (9/5)
= (8 × 9)/(7 × 50
= 63/35
b. (2/3) : (4/5)
= (2/3) × (5/4)
= (2 × 5) × (3 × 4)
= 10/12
= 5/6
c. ¾ : ½
= ¾ × 2/1
= (3 × 2)/(4 × 1)
= 6/4
= 3/2
= 1½
d. (3/5) : (2/3)
= (3/5) × (3/2)
= (3 × 3)/(5 × 2)
= 9/10
Demikian postingan Mafia Online tentang operasi pembagian
bilangan pecahan. Mohon maaf jika ada kata atau perhitungan yang salah dalam
postingan ini. Salam Mafia => Kita pasti bisa.
....
BalasHapus____ = 9÷10
.....