Konsep dasar yang kamu harus kuasai untuk memahami materi gerak benda yang dihubungkan dengan tali melalui katrol adalah hukum II Newton. Oke langsung saja ke pembahasan. Perhatikan Gambar 1 di bawah ini.

Gambar 1 merupakan dua buah benda m1 dan m2
yang dihubungkan dengan tali melalui katrol. Jika tidak ada gesekan antara
katrol dengan tali (katrol licin), adapun gaya-gaya yang bekerja pada sistem
tersebut terlihat seperti gambar 2. Jika kita anggap katrol bergerak dengan m1
naik ke atas dan m2 bergerak ke bawah seperti Gambar 3. Untuk
yang mengarah ke atas kita beri nilai positif dan bergerak ke bawah kita beri
nilai negatif, maka:
Untuk sistem m1 akan berlaku hukum II Newton
yakni:
∑F1 = m.a
T1 – w1 = m1.a
T1 – m1.g = m1.a
T1 = m1.g + m1.a
Sedangkan untuk sistem m2 akan berlaku hukum
II Newton (dengan a mengarah ke bawah) yakni:
∑F2 = – m2.a
T2 – w2 = – m2.a
T2 – m2.g = – m2.a
T2 = m2.g – m2.a
Oleh karena tidak ada gesekan antara tali dengan katrol,
sehingga semua tegangan tali sama besar (T1 = T2), maka:
m1.g + m1.a = m2.g – m2.a
m1.a + m2.a = m2.g – m1.g
a(m1 + m2) = (m2 – m1)g
a = (m2 – m1)g/(m1 + m2)
Perhatikan gambar di bawah ini!

Sebuah benda m1 diletakan di atas meja,
kemudian dihubungkan dengan tali melalui katrol dengan benda m2.
Jika tidak ada gesekan antara tali denga katrol maka:
Untuk sistem m1 akan berlaku hukum II Newton
yakni:
∑F1 = m.a
Karena sistem pada m1 bergerak secara
horizontal (ke kanan) maka pengaruh gaya berat diabaikan (benda m1
tidak bergerak secara vertikal), maka:
T1 = m1.a
Sedangkan untuk sistem m2 akan berlaku hukum
II Newton (dengan a mengarah ke bawah) yakni:
∑F2 = – m2.a
T2 – w2 = – m2.a
T2 – m2.g = – m2.a
T2 = m2.g – m2.a
Oleh karena tidak ada gesekan antara tali dengan katrol,
sehingga semua tegangan tali sama besar (T1 = T2), maka:
m1.a = m2.g – m2.a
m1.a + m2.a = m2.g
a(m1 + m2) = m2.g
a = m2.g/(m1 + m2)
Untuk memantapkan pemahaman kamu tentang gerak benda yang
dihubungkan dengan tali melalui katrol silahkan simak contoh soal di bawah ini.
Contoh
Soal 1
Dua benda A dan B masing-masing 6 kg dan 4 kg dihubungkan
dengan tali melalui sebuah katrol yang licin seperti gambar di bawah ini.

Hitunglah percepatan dan tegangan tali jika kedua benda
dilepaskan (g = 10 m/s2)!
Penyelesaian:
Jika kedua benda dilepaskan, A bergerak ke bawah dan B
bergerak ke atas karena massa A lebih besar dari massa B, kedua benda akan
bergerak dengan percepatan yang sama. Perhatikan gambar di bawah ini.

Untuk sistem mA (a mengarah ke bawah) akan
berlaku hukum II Newton yakni:
∑FA= mA. – a
∑FA= – mA. a
TA – wA = – mA. a
TA – mA.g = – mA.a
TA = mA.g – mA.a
TA = 6.10 – 6.a
TA = 60 – 6a
Sedangkan untuk sistem mB (a mengarah ke atas)
akan berlaku hukum II Newton yakni:
∑FB = mB.a
TB – wB = mB.a
TB – mB.g = mB.a
TB = mB.g + mB.a
TB = 4.10 + 4.a
TB = 40 + 4a
Antara tali dengan katrol tidak ada gesekan, sehingga
semua tegangan tali sama besar (TA = TB), maka:
60 – 6a = 40 + 4a
60 – 40 = 6a + 4a
20 = 10a
a = 20/10
a = 2 m/s2
Tegangan tali dapat dihitung dengan menggunakan persamaan
pada sistem mA, yakni:
TA = 60 – 6a
TA = 60 – 6(2)
TA = 60 – 12
TA = 48 N
Atau dapat juga dihitung dengan menggunakan persamaan
pada sistem mB, yakni:
TB = 40 + 4a
TB = 40 + 4(2)
TB = 40 + 8
TB = 48 N
Jadi, percepatan dan tegangan tali jika kedua benda
dilepaskan adalah 2 m/s2 dan 48 N.
Contoh
Soal 2
Tiga benda A, B dan C masing-masing memiliki masa 4 kg, 15
kg dan 6 kg dihubungkan dengan sebuah tali melalui katrol yang licin seperti
gambar di bawah ini.

Jika g = 10 m/s2, tentukan:
a. percepatan sistem jika ketiga benda dilepaskan
b. tegangan tali antara benda A dan C
c. tegangan tali pada benda B!
Penyelesaian:
Jika ketiga benda dilepaskan, A dan C akan bergerak ke
atas dan B bergerak ke bawah karena massa B lebih besar dari massa A ditambah
massa C dan ketiga benda akan bergerak dengan percepatan yang sama. Perhatikan
gambar di bawah ini.
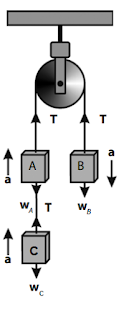
Untuk sistem mc (a mengarah ke atas) akan
berlaku hukum II Newton yakni:
∑Fc= mc.a
Tc – wc = mc. a
Tc – mc.g = mc.a
Tc = mc.g + mc.a
Tc = 6.10 + 6.a
Tc = 60 + 6a
Untuk sistem mA (a mengarah ke atas) akan
berlaku hukum II Newton yakni:
∑FA= mA.a
TA – wA – Tc = mA.a
TA – mA.g – Tc = mA.a
TA = mA.a + mA.g + Tc
TA = 4.a + 4.10 + Tc
TA = 4a + 40 + Tc
Substitusi Tc, maka:
TA = 4a + 40 + Tc
TA = 4a + 40 + 60 + 6a
TA = 10a + 100
Untuk sistem mB (a mengarah ke bawah) akan
berlaku hukum II Newton yakni:
∑FB= mB. –a
TB – wB = –mB.a
TB – mB.g = –mB.a
TB = mB.g – mB.a
TB = 15.10 – 15.a
TB = 150 – 15a
a. antara tali dengan katrol tidak ada gesekan, sehingga
TA = TB, maka:
TA = TB
10a + 100 = 150 – 15a
25a = 50
a = 50/25
a = 2 m/s2
Jadi, percepatan sistem tersebut adalah 2 m/s2.
b. tegangan tali antara benda A dan C adalah TC
yakni:
Tc = 60 + 6a
Tc = 60 + 6(2)
Tc = 60 + 12
Tc = 72 N
Jadi, tegangan tali antara benda A dan C adalah 72 N
c. tegangan tali pada benda B adalah TB yakni:
TB = 150 – 15a
TB = 150 – 15(2)
TB = 150 – 30
TB = 120 N
Atau bisa juga
mencarinya melalui sistem mA yakni:
TA = 4a + 40 + Tc
TA = 4(2) + 40 + 72
TA = 120 N
Jadi tegangan tali pada benda B adalah 120 N
Contoh
Soal 3
Dua benda A dan B masing-masing memiliki masa 4 kg dan 6
kg dihubungkan dengan sebuah tali melalui katrol yang licin seperti gambar di
bawah ini.

Jika tidak ada gesekan antara benda A dengan bidang
sentuh (meja), hitunglah percepatan dan tegangan tali jika kedua benda
dilepaskan (g = 10 m/s2)!
Penyelesaian:
Jika benda A dan B dilepaskan secara bersamaan maka benda
B akan bergerak ke bawah dan benda A akan bergerak ke kanan dengan percepatan
yang sama. Perhatikan gambar di bawah ini.

Untuk sistem mA (a mengarah ke kanan) akan
berlaku hukum II Newton yakni:
∑FA= mA.a
TA = mA. a
TA = 4a
Untuk sistem mB (a mengarah ke bawah) akan
berlaku hukum II Newton yakni:
∑FB= mB. –a
TB – wB = –mB.a
TB – mB.g = –mB.a
TB = mB.g – mB.a
TB = 6.10 – 6.a
TB = 60 – 6a
Antara tali dengan katrol tidak ada gesekan, sehingga TA
= TB, maka:
TA = TB
4a = 60 – 6a
10a = 60
a = 60/10
a = 6 m/s2
Jadi, percepatan sistem tersebut adalah 6 m/s2.
Tegangan tali dapat dihitung dengan menggunakan persamaan
pada sistem mA, yakni:
TA = 4a
TA = 4(6)
TA = 24 N
Atau dapat juga dihitung dengan menggunakan persamaan
pada sistem mB, yakni:
TB = 60 – 6a
TB = 60 – 6(6)
TB = 60 – 36
TB = 24 N
Jadi, percepatan dan tegangan tali jika kedua benda
dilepaskan adalah 6 m/s2 dan 24 N.
Contoh
Soal 4
Tiga benda A, B, dan C memiliki massa masing-masing 2 kg,
3 kg dan 5 kg dihubungkan dengan tali melalui sebuah katrol yang licin seperti
gambar di bawah ini.

Jika g = 10 m/s2, tentukan:
a. percepatan sistem jika ketiga benda dilepaskan
b. tegangan tali antara benda A dan B
c. tegangan tali pada benda C!
Penyelesaian:
Jika ketiga benda dilepaskan, A dan B akan bergerak ke
kanan dan C bergerak ke bawah dan ketiga benda akan bergerak dengan percepatan
yang sama. Perhatikan gambar di bawah ini.

Untuk sistem mA (a mengarah ke kanan) akan
berlaku hukum II Newton yakni:
∑FA= mA.a
T1 = mA. a
T1 = 2a
Untuk sistem mB (a mengarah ke kanan) akan
berlaku hukum II Newton yakni:
∑FB= mB.a
T2 – T1 = mB.a
T2 – 2a = 3a
T2 = 5a
Untuk sistem mC (a mengarah ke bawah) akan
berlaku hukum II Newton yakni:
∑FC = mC. –a
T3 – wC = –mC.a
T3 – mC.g = –mC.a
T3 = mC.g – mC.a
T3 = 5.10 – 5.a
T3 = 50 – 5a
a. antara tali dengan katrol tidak ada gesekan, sehingga
T2 = T3, maka:
T2 = T3
5a = 50 – 5a
10a = 50
a = 50/10
a = 5 m/s2
Jadi, percepatan sistem tersebut adalah 5 m/s2.
b. tegangan tali antara benda A dan B adalah T1
yakni:
T1 = 2a
T1 = 2(5)
T1 = 10 N
Jadi, tegangan tali antara benda A dan B adalah 10 N
c. tegangan tali pada benda C adalah T3 atau T2
karena T3 = T2, maka:
T3 = 50 – 5a
T3 = 50 – 5(5)
T3 = 25 N
Atau bisa juga mencarinya melalui T2 yakni:
T2 = 5a
T2 = 5(5)
T2 = 25 N
Jadi tegangan tali pada benda B adalah 25 N
Contoh
Soal 5
Dua benda A dan B yang memiliki massa masing-masing 20
dan 5 kg yang dihubungkan dengan sebuah katrol yang licin seperti gambar di
bawah ini.

Jika tidak ada gesekan antara benda A dengan permukaan
bidang miring (pemukaan licin), tentukan percepatan sistem dan tegangan tali
jika kedua benda dilepaskan secara bersama-sama (g = 10 m/s2)!
Penyelesaian:
Jika kedua benda dilepaskan, kita prediksi benda A akan menaiki
bidang miring dan benda B akan turun dengan percepatan yang sama, seperti
gambar di bawah ini.

Untuk sistem pada benda A akan berlaku hukum II Newton
yakni:
∑FA= mA.a
T – mA.g.sin α = mA.a
T – 20.10.sin 30° = 20a
T – 100 = 20a
T = 100 + 20a
Untuk sistem pada benda B akan berlaku hukum II Newton
yakni:
T – mB.g = mB. – a (a negatif
karena ke bawah)
T – 5.10 = – 5a
T = 50 – 5a
antara tali dengan katrol tidak ada gesekan, sehingga
tegangan tali pada benda A sama dengan tegangan tali pada benda B, maka:
T = T
100 + 20a = 50 – 5a
20a + 5a = 50 – 100
25a = –50
a = -50/25
a = –2 m/s2 (a bernilai negatif berarti arah
pergerakan sistem terbalik dari yang diprediksi, sehingga benda A menuruni bidang
miring dan benda B bergerak ke atas dengan percepatan yang sama).
Tegangan tali pada sistem dapat ditinjau dari benda A
yakni:
T = 100 + 20a
T = 100 + 20(–2)
T = 100 – 40
T = 60 N
atau bisa juga ditinjau dari benda B yakni:
T = 50 – 5a
T = 50 – 5(–2)
T = 50 + 10
T = 60 N
Jadi, percepatan sistem dan tegangan tali jika kedua
benda dilepaskan secara bersama-sama yakni 2 m/s2 dan 60 N dengan
benda B bergerak ke atas.
Bagaimana? Mudah bukan? Jika ada kendala atau permasalah dalam memahami gerak benda yang dihubungkan dengan tali melalui katrol, silahkan tanyakan di kolom komentar.
0 Response to "Gerak Benda yang Dihubungkan dengan Tali Melalui Katrol"
Posting Komentar
Terima kasih sudah membaca blog ini, silahkan tinggalkan komentar dengan sopan dan tidak mengandung unsur SARA atau pornografi serta tidak ada link aktif. Mohon maaf kalau komentarnya dibalas agak lambat. Kolom komentar ini kami moderasi, jadi kalau ada komentar yang tidak sesuai dengan ketentuan tidak akan dipublikasikan.