Cara Menentukan Jarak Titik Ke Titik Pada Kubus

Agar bisa menentukan jarak titik ke titik pada kubus ada beberapa konsep yang bisa kamu gunakan yakni konsep diagonal bidang, konsep diagonal ruang, dan teorema Pythagoras.

 

Contoh Soal 1

Pada kubus ABCD.EFGH, panjang rusuk 9 cm. Tentukan jarak titik D ke titik F.

 

Penyelesaian:

Untuk memudahkan menyelesaikan soal tersebut, kamu harus menggambarnya terlebih dahulu, maka akan tampak seperti gambar di bawah ini.

Kubus ABCD.EFGH

 

Jarak titik B ke titik F merupakan garis diagonal ruang kubus. Untuk menyelesaiakannya bisa menggunakan Teorema Pythagoras. Terlebih dahulu cari panjang BD. Perhatikan segitiga siku-siku ABD, maka:

BD² = AB² + AD²

BD² = 9² + 9²

BD² = 81 + 81

BD² = 162

BD = 9√2 cm

 

Kemudian cari panjang DF. Perhatikan segitiga siku-siku BDF, maka:

DF² = BD² + BF²

DF² = (9√2)² + 9²

DF² = 162 + 81

DF² = 243

DF = √243

DF = 9√3 cm

Jadi jarak titik D ke titik F adalah 9√3 cm.

 

Cara Cepat:

Selain menggunakan teorema Pytagoras, soal di atas bisa menggunakan rumus diagonal ruang kubus. Jika sebuah kubus memiliki rusuk r, maka diagonal ruangnya dapat dirumuskan:

d = r√3

 

Jarak titik D ke titik F merupakan panjang diagonal ruang kubus. Jika panjang rusuk 9 cm, maka:

d = r√3

d = 9√3 cm

 

Contoh Soal 2

Diketahui kubus ABCD.EFGH memiliki rusuk 4 cm. Ttitik P merupakan diagonal bidang ABCD dan titik Q merupakan diagonal bidang EFGH. Jika titik R berada di tengah-tenagah garis PQ, maka tentukan jarak titik R ke titik G!

 

Penyelesaian:

Jika soal di atas diilustrasikan ke dalam gambar maka akan tampak seperti gambar di bawah ini.

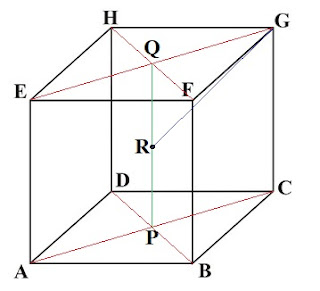
Perhatikan segitiga RGQ yang merupakan segitiga siku-siku. Cari terlebih dahulu panjang EG dengan teorema Pytagoras, maka:

EG² = EF² + FG²

EG² = 4² + 4²

EG² = 16 + 16

EG² = 32

EG = √32

EG = 4√2 cm

 

Panjang GQ merupakan setengah panjang EG, maka:

GQ = ½ EG

GQ = ½ (4√2 cm)

GQ = 2√2 cm

 

Panjang QR merupakan setengah panjang PQ atau setengah panjang rusuk kubus, maka:

QR = ½ PQ

QR = ½ (4 cm)

QR = 2 cm

 

Panjang GR dapat dicari dengan Teorema Pytagoras, yakni:

GR² = QR² + GQ²

GR² = 2² + 2√2²

GR² = 4 + 8

GR² = 12

GR = √12

GR = 2√3 cm

 

Cara Cepat:

Selain menggunakan Teorema Pythagoras, mencari jarak titik R ke titik G bisa menggunakan rumus panjang diagonal ruang kubus. Perhatikan kembali gambar di atas. Panjang GR merupakan setengah panjang AG yang merupakan panjang diagonal ruang kubus, maka:

d = ½ r√3

d = ½ (4 cm)√3

d = 2√3 cm

Jadi, jarak titik R ke titik G adalah 2√3 cm.

 

Bagaimana? Mudah bukan? Jika ada kendala dalam memahami menentukan jarak titik ke titik pada kubus, silahkan tanyakan di kolom komentar.

TOLONG DIBAGIKAN YA :