Mencari Panjang Tali Busur Pada Lingkaran Dengan Aturan Sinus

Sebelumnya admin sudah membahas cara mencari panjang tali busur pada lingkaran jika sudut pusatnya 90 drajat (90°). Dari postingan tersebut memunculkan pertanyaan “Bagaimana menentukan panjang tali busur pada lingkaran apabila sudut pusatnya bukan 90 derajat”

 

Perhatikan Gambar 1 di bawah ini.

Tali busur AB pada lingkaran

Tali busur lingkaran tersebut ditunjukkan oleh garis lurus AB yang tidak melalui titik pusat seperti pada gambar di atas. Untuk memudahkan memahaminya perhatikan pada segitiga AOB yang merupakan segitiga sama kaki. Jika di tarik garis dari titik O ke tepat di tengah-tengah garis AB maka sudut α terbagi menjadi dua.

 

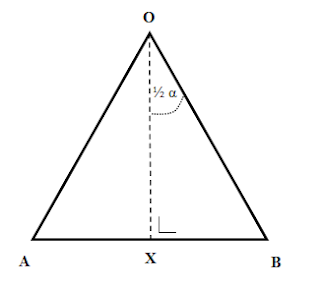
Sekarang perhatikan Gambar 2 di bawah ini.

 

Segitiga AOB

Perhatikan segitiga BOX yang merupakan segitiga siku-siku dengan sudut BOX = ½α. Kita cari panjang BX dengan menggunakan aturan sinus yakni:

Sin (½α) = BX/BO

BX = BO.sin (½α)

 

Sekarang panjang tali busur lingkaran dapat dicari yakni:

Panjang AB = 2BX

Panjang AB = 2.BO.sin (½α)

 

Jadi rumus untuk mencari panjang tali busur pada lingkaran dengan sudut pusat α yakni:

Tali Busur = 2 x jari-jari lingkaran x sin (½α)

 

atau

 

TB = 2r.sin (½α)

 

Untuk memantapkan pemahaman kamu tentang cara mencari panjang tali busur pada lingakaran dengan sudut pusat α dengan aturan sinus silahkan simak contoh soal di bawah ini.

 

Contoh Soal 1

Sebuah lingkaran dengan sudut pusat 90° memiliki panjang jari-jari 5 cm tentukan panjang tali busur lingkaran tersebut (sin 45° = ½ √2).

 

Penyelesaian:

r  = 5 cm

α = 90°

 

TB = 2r.sin (½α)

TB = 2(5 cm)(sin (½.90°))

TB = 2(5 cm)(sin 45°)

TB = 10 cm. ½ √2

TB = 5√2 cm

 

Jadi panjang tali busur pada lingkaran tersebut adalah 5√2 cm.

 

Contoh Soal 2

Sebuah lingkaran dengan sudut pusat 60° memiliki panjang jari-jari 10 cm tentukan panjang tali busur lingkaran tersebut (sin 30° = 0,5).

 

Penyelesaian:

r = 10 cm

α = 60°

 

TB = 2r.sin (½α)

TB = 2(10 cm).sin (½.60°)

TB = 2(10 cm).sin 30°

TB = 20 cm . 0,5

TB =  10 cm

 

Jadi panjang tali busur pada lingkaran tersebut adalah 10 cm.

 

Contoh Soal 3

Perhatikan Gambar 3 di bawah ini

Contoh soal tali busur

Jika sin 15° = 0,26 tentukan panjang tali busur AB!

 

Penyelesaian:

r = 5 cm

α = 30°

 

AB = 2r.sin (½α)

AB = 2(5 cm).sin (½.30)

AB = 10 cm . sin 15°

AB = 10 cm . 0,26

AB = 2,6 cm

 

Jadi panjang tali busur AB adalah 2,6 cm

 

Demikian artikel cara mencari panjang tali busur pada lingkaran dengan menggunakan aturan sinus. Jika ada yang belum dipahami terkait materi ini, silahkan ditanyakan di kolom komentar.

TOLONG DIBAGIKAN YA :