Konsep dasar yang harus kamu kuasai agar bisa menentukan sistem persamaan linear dari grafik yakni menentukan gradien atau kemiringan suatu garis. Di mana persamaan suatu garis dengan kemiringan atau gradien (m) tertentu dapat ditulis dengan persamaan:
y = mx + c
Bagaimana cara mencari kemiringan atau gradien suatu
garis linear? Kemiringan suatu garis atau gradien garis dapat ditentukan dengan
menggunakan rumus:
m = (y2 – y1)/(x2 – x1)
Jadi sebelum mencari kemiringan garis, kamu harus
menentukan dua titik koordinat xy yang dilalui garis tersebut yakni (x1,y1)
dan (x2,y2). Oke, agar lebih mudah memahaminya, silahkan
simak contoh soal di bawah ini.
Contoh
Soal
Perhatikan gambar grafik berikut ini.
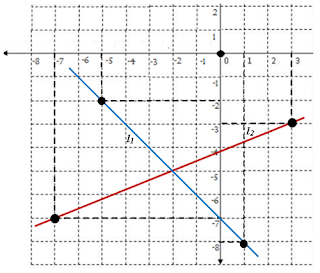
Tentukan sistem persamaan linear dan penyelesaiannya pada
gambar di atas.
Penyelesaian:
Gambar di atas terdapat dua buah garis (l1 dan l2) yang berpotongan disebuah titik. Cari terlebih
dahulu persamaan garis l1 dan
l2 dengan mencari
kemiringan masing-masing garis.
Untuk
garis l1:
Garis l1
melalui titik (-5, -2) dan titik (1.-8). Gradien garisnya yakni:
m = (y2 – y1)/(x2 – x1)
m = (-8 – (-2))/(1 – (-5))
m = -6/6
m = – 1
Substitusi salah satu titik ke persamaan garis liniear.
Misalkan titik (-5,-2), maka:
y = mx + c
-2 = (-1)(-5) + c
-2 = 5 + c
c = - 7
Jadi persamaan garis untuk l1 yakni:
y = mx + c
y = -x - 7
atau
x + y = -7
Untuk
garis l2:
Garis l2
melalui titik (-7, -7) dan titik (3.-3). Gradien garisnya yakni:
m = (y2 – y1)/(x2 – x1)
m = (-3 – (-7))/(3 – (-7))
m = 4/10
m = 2/5
Substitusi salah satu titik ke persamaan garis liniear.
Misalkan titik (-7,-7), maka:
y = mx + c
-7 = (2/5)(-7) + c
-7 = -14/5 + c
-35/5 = -14/5 + c
c = - 35/5 + 14/5
c = - 21/5
Jadi persamaan garis untuk l2 yakni:
y = mx + c
y = (2/5)x – 21/5 <= dikali 5, maka:
5y = 2x - 21
atau
-2x + 5y = -21
Jadi sistem persamaan linear dari grafik di atas yakni:
-2x + 5y = -21
x + y = -7
Di koordinat mana titik potong garis tersebut? Nah untuk
mencari titik potongnya dapat menggunakan metode substitusi. Titik potong di
titik x yakni:
-2x + 5y = -21
-2x + 5(-x – 7) = -21
-2x - 5x – 35 = -21
-7x = 14
x = 14/-7
x = -2
Titik potong di titik y yakni:
y = -x - 7
y = -(-2) – 7
y = 2 – 7
y = – 5
Jadi penyelesaian sistem persamaan linear dari grafik di
atas yakni {- 2, -5}
Demikian artikel tentang cara menentukan sistem persamaan
linear dari grafik. Jika ada masalah dalam memahami materi ini, silahkan
tanyakan di kolom komentar.
0 Response to "Cara Menentukan Sistem Persamaan Linier Dari Grafik"
Posting Komentar
Terima kasih sudah membaca blog ini, silahkan tinggalkan komentar dengan sopan dan tidak mengandung unsur SARA atau pornografi serta tidak ada link aktif. Mohon maaf kalau komentarnya dibalas agak lambat. Kolom komentar ini kami moderasi, jadi kalau ada komentar yang tidak sesuai dengan ketentuan tidak akan dipublikasikan.