Menentukan Vektor Posisi Dari Fungsi Kecepatan

Sebelumnya admin sudah membahas tentang kecepatan sesaat dalam satu dimensi dan kecepatan sesaat dua dimensi yang diturunkan (didiferensialkan) dari fungsi vektor posisi. Nah sekarang Mafia Online, akan membahas cara menentukan posisi suatu partikel dengan menurunkan fungsi kecepatannya. Konsep dasar yang kamu harus kuasai dalam memahami materi ini adalah konsep intergral. 

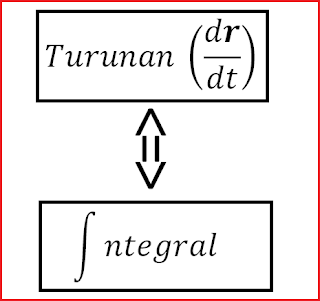
Integral merupakan kebalikan dari turunan (diferensial). Adapun rumus integral secara matematis adalah:

r = ∫xⁿ dx

r = (xⁿ⁺¹)/1+n

Untuk memantapkan pemahaman konsep integral silahkan simak contoh soal di bawah ini.

r = ∫8t³ dt

r = (8tⁿ⁺¹)/1+n

r = (8t³⁺¹)/1+3

r = (8t⁴)/4

r = 2t⁴

Dalam arah sumbu-x, fungsi kecepatan suatu benda dapat diturunkan dari fungsi posisi yakni:

v_x = dx/dt

Bagaimana menentukan fungsi posisi dari fungsi kecepatan? Posisi benda dapat dicari dengan mengintegralkan fungsi kecepatan, silahkan simak uraian berikut.

v_x =dx/dt

dx = v_x dt

dengan mengintegralkan kedua ruas maka:

∫dx = ∫ v_x dt

Batas-batas integral untuk ruas kiri yakni untuk batas atas sebesar x dan batas bawah sebesar x₀, sedangkan batas-batas integral untuk ruas kanan yakni untuk batas atas sebesar t dan batas bawah sebesar t₀, maka persamaannya menjadi:

∫dx = ∫ v_x dt

x – x₀  = ∫ v_x dt

x = x₀ + ∫ v_x dt

hal ini berlaku juga untuk sumbu-y, fungsi kecepatan suatu benda dapat diturunkan dari fungsi posisi yakni:

v_y = dy/dt

dy = v_y dt

dengan mengintegralkan kedua ruas maka:

∫dy = ∫ v_y dt

Batas-batas integral untuk ruas kiri yakni untuk batas atas sebesar y dan batas bawah sebesar y₀, sedangkan batas-batas integral untuk ruas kanan yakni untuk batas atas sebesar t dan batas bawah sebesar t₀, maka persamaannya menjadi:

∫dy = ∫ v_y dt

y – y₀  = ∫ v_y dt

y = y₀ + ∫ v_y dt

Dalam hal ini (x₀, y₀) menyatakan koordinat posisi awal benda, sedangkan (x, y) menyatakan koordinat posisi benda setelah bergerak dalam selang waktu t. Apabila dituliskan dalam bentuk vektor, posisi benda dapat dituliskan sebagai berikut

r = xi + yj

dengan memasukan x dan y, maka diperoleh:

r = (x₀ + ∫ v_x dt)i + (y₀ + ∫ v_y dt)j

Untuk memantapkan pemahaman kamu tentang cara menentukan vektor posisi dari fungsi kecepatan, silahkan simak contoh soal di bawah ini.

Contoh Soal

Sebuah partikel bergerak pada bidang xy. Pada posisi awal (x₀,y₀), partikel berada pada koordinat (4,1) m. Pada sumbu-x kecepatan partikel memenuhi persamaan v_x = 5 + 6t dan pada sumbu-y kecepatan partikel memenuhi persamaan v_y = 3 + 4t, dengan v_x dan v_y dalam m/s, dan t dalam sekon. Tentukanlah:

a. persamaan umum vektor posisi partikel,

b. posisi partikel pada saat t = 2 sekon, dan

c. perpindahan partikel antara t = 1 dan t = 3 sekon.

Penyelesaian:

a. Posisi awal partikel adalah (4,1) m, maka x₀ = 4 m dan y₀ = 1 m. Dengan demikian persamaan umum vektor posisi partikel yakni:

r = (x₀ + ∫ v_x dt)i + (y₀ + ∫ v_y dt)j

r = [4 + ∫(5 + 6t)dt]i + [1 + ∫(3 + 4t)dt]j

r = (4 + 5t + 3t²)i + (1 + 3t + 2t²)j

b. Posisi partikel pada saat t = 2 sekon yakni:

=> pada sumbu-x

x = 4 + 5t + 3t²

x = 4 + 5.2 + 3.2²

x = 4 + 10 + 12

x = 26 m

=> pada sumbu-y

y = 1 + 3t + 2t²

y = 1 + 3.2 + 2.2²

y = 1 + 6 + 8

y = 15 m

Jadi, vektor posisi partikel pada saat t = 2 adalah r = (26i + 15j) m

c. posisi partikel di t = 1 sekon yakni:

r = (4 + 5t + 3t²)i + (1 + 3t + 2t²)j

r₁ = (4 + 5.1 + 3.1²)i + (1 + 3.1 + 2.1²)j

r₁ = (12i + 6j) m

posisi partikel di t = 3 sekon yakni:

r = (4 + 5t + 3t²)i + (1 + 3t + 2t²)j

r₃ = (4 + 5.3 + 3.3²)i + (1 + 3.3 + 2.3²)j

r₃ = (46i + 28j) m

Perpindahan partikel dari t = 1 sekon hingga t = 3 sekon adalah

Δr = r₃ – r₁

Δr = (46i + 28j) m – (12i + 6j) m

Δr = (34i + 22j) m

Demikian pembahasan materi dan contoh soal tentang cara menentukan vektor posisi dari fungsi vektor kecepatan. Mohon maaf jika ada kata-kata dan perhitungan yang salah dalam postingan ini. Jika ada kendala dalam memahami materi ini, silahkan tanyakan pada kolom komentar. Salam mafia => kita pasti bisa.

TOLONG DIBAGIKAN YA :