Kecepatan Rata-Rata Dalam Satuan Vektor

Sebelumnya admin sudah membahas tentang kecepatan sesaat dalam satu dimensi dan kecepatan sesaat dalam dua dimensi serta dilengkapi dengan beberapa contoh soalnya. Postingan kali ini masih membahas tentang kecepatan yakni kecepatan rata-rata dalam satuan vektor. Sebenarnya materi tentang kecepatan rata-rata sudah dipelajari waktu di kelas X, sedangkan pada materi kali ini admin akan membahas analisis kecepatan rata-rata ditinjau dari perhitungan vektor.

Kita ketahui bahwa secara matematis, kecepatan didefinisikan sebagai perubahan posisi (perpindahan) per satuan waktu. Lalu bagaimana dengan kecepatan rata-rata dengan satuan vektor? Silahkan perhatikan gambar di bawah ini.

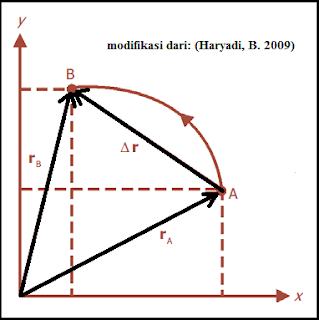Perubahan posisi benda dari titik A ke titik B dalam waktu Δt

Berdasarkan gambar di atas diketahui bahwa sebuah benda (partikel) dari titik A dengan vektor posisi r_A kemudian berpindah posisi ke titik B dengan vektor posisi r_B. Perubahan posisi dari titik A ke titik B dinyatakan dengan Δr, di mana Δr = r_B – r_A. silahkan baca materi perpindahan dengan vektor satuan. Benda berpindah dari titik A ke titik B memerlukan waktu sebesar Δt, di mana Δt = t_B – t_A.

Berdasarkan definisi matematis kecepatan, maka dapat ditulis:

v = (r_B – r_A)/(t_B – t_A)

v = Δr/Δt

Nah persamaan v = Δr/Δt merupakan persamaan kecepatan rata-rata secara umum. Lalu bagaimana persamaan kecepatan rata-rata untuk satuan vektor?

Jika kecepatan rata-rata benda dalam bidang xy, dapat dicari dengan cara memasukkan nilai Δr dalam bentuk satuan vektor, di mana Δr = Δxi + Δyj, maka:

v = Δr/Δt

v = (Δxi + Δyj)/Δt

v = (Δx/Δt)i + (Δy/Δt)j

jika Δx/Δt = v_x dan Δy/Δt = v_y, maka:

v = v_x i + v_y j

Sedangkan untuk mencari besar kecepatan rata-rata benda tersebut, dapat dihitung dengan menggunakan persamaan:

I v I = √[(v_x)² + (v_y)²]

Arah kecepatan rata-rata benda terhadap sumbu-x dinyatakan dengan θ, di mana besar θ secara matematis, dapat ditulis:

tan θ = v_x/v_y

θ = arc tan (v_x/v_y)

Untuk memantapkan pemahaman kamu tentang materi kecepatan rata-rata dengan satuan vektor, silahkan simak contoh soal di bawah ini.

Contoh Soal 1

Sebuah partikel bergerak dalam bidang xy dengan persamaan x = t² + 4t – 1 dan y = t² + 2t, x dan y dalam meter dan t dalam sekon. Tentukan posisi, kecepatan rata-rata, dan besar kecepatan rata-rata benda dalam selang waktu pada waktu t = 1 sekon hingga t = 3 sekon.

Penyelesaian:

Posisi benda dinyatakan dengan r maka:

r = xi + yj

r = (t² + 4t – 1)i + (t² + 2t)j

Untuk mencari posisi benda dengan cara memasukan nilai t ke persamaan r, maka:

=> Untuk t = 1 yakni:

r₁ = (t² + 4t – 1)i + (t² + 2t)j

r₁ = (1² + 4.1 – 1)i + (1² + 2.1)j

r₁ = (1 + 4 – 1)i + (1 + 2)j

r₁ = (4i + 3j) m

=> Untuk t = 3 yakni:

r₃ = (t² + 4t – 1)i + (t² + 2t)j

r₃ = (3² + 4.3 – 1)i + (3² + 2.3)j

r₃ = (9 + 12 – 1)i + (9 + 6)j

r₃ = (20i + 15j) m

Untuk mencari posisi benda dengan cara memasukan nilai t ke persamaan r, maka:

=> Untuk t = 1 yakni:

r₁ = (t² + 4t – 1)i + (t² + 2t)j

r₁ = (1² + 4.1 – 1)i + (1² + 2.1)j

r₁ = (1 + 4 – 1)i + (1 + 2)j

r₁ = (4i + 3j) m

=> Untuk t = 3 yakni:

r₃ = (t² + 4t – 1)i + (t² + 2t)j

r₃ = (3² + 4.3 – 1)i + (3² + 2.3)j

r₃ = (9 + 12 – 1)i + (9 + 6)j

r₃ = (20i + 15j) m

Sedangkan untuk mencari kecepatan rata-rata benda dalam selang waktu pada waktu t = 1 sekon hingga t = 3 sekon, terlebih dahulu mencari Δr yakni:

Δr = r₃ – r₁

Δr = (20i + 15j)  – (4i + 3j)

Δr = (16i + 12j) m

Perubahan waktu:

Δt = t₃ – t₁

Δt = 3 – 1

Δt = 2 s

v = Δr/Δt

v = (16i + 12j)/2

v = (8i + 6j) m/s

Besar kecepatan rata-rata dalam selang waktu t = 1 sekon hingga t = 3 sekon, yakni:

I v I = √[(v_x)² + (v_y)²]

I v I = √[(8)² + (6)²]

I v I = √(64 + 36)

I v I = √(100)

I v I = 10 m/s

Contoh Soal 2

Sebuah partikel bergerak pada bidang xy dengan persamaan x = t² + 3 dan y = t – t², x dan y dalam meter dan t dalam sekon. Tentukan arah kecepatan rata-rata dalam selang waktu t = 1 hingga t = 3.

Penyelesaian:

Posisi benda dinyatakan dengan r maka:

r = xi + yj

r = (t² + 3)i + (t – t²)j

Untuk mencari posisi benda dengan cara memasukan nilai t ke persamaan r, maka:

=> Untuk t = 0 yakni:

r₁ = (t² + 3)i + (t – t²)j

r₁ = (1² + 3)i + (1 – 1²)j

r₁ = 4i

=> Untuk t = 3 yakni:

r₃ = (t² + 3)i + (t – t²)j

r₃ = (3² + 3)i + (3 – 3²)j

r₃ = (9 + 3)i + (3 – 9)j

r₃ = (12i – 6j) m

Sedangkan untuk mencari kecepatan rata-rata benda dalam selang waktu pada waktu t = 1 sekon hingga t = 3 sekon, terlebih dahulu mencari Δr yakni:

Δr = r₃ – r₁

Δr = (12i – 6j)  – 4i

Δr = (8i – 6j) m

Perubahan waktu:

Δt = t₃ – t₁

Δt = 3 – 1

Δt = 2 s

v = Δr/Δt

v = (8i – 6j)/2

v = (4i – 3j) m/s

Arah kecepatan rata-rata benda yakni:

tan θ = v_x/v_y

tan θ = 4/–3

tan θ = 4/–3

θ = arc tan (4/–3)

θ = 126,8°

Jadi arah kecepatan rata-rata dalam rentang waktu dari t = 1 sekon hingga t = 3 sekon adalah 126,8°.

Demikian pembahasan materi dan contoh soal tentang kecepatan rata-rata dengan satuan vektor. Mohon maaf jika ada kata-kata dan perhitungan yang salah dalam postingan ini. Jika ada kendala dalam memahami materi ini, silahkan tanyakan pada kolom komentar. Salam mafia => kita pasti bisa.

TOLONG DIBAGIKAN YA :