Pada postingan Materi Mafia Online kali ini,
akan membahas tentang konsep perbandingan trigonometri pada suatu segitiga
siku-siku. Dalam kehidupan sehari-hari sering kita jumpai bentuk segitiga siku-siku,
misalnya pada saat meletakkan posisi tangga pada tembok seperti gambar di bawah ini.
 |
| Tangga bersandar pada tembok Sumber: youtube.com |
Jika kita gambarkan antara ujung tangga atas
dengan tembok, ujung bawah tangga dengan tanah atau lantai, dan tanah dengan
tembok akan membentuk sebuah segitiga siku-siku seperti gambar di bawah ini.
 |
| Segitiga siku-siku |
Gambar di atas merupakan bangun segitiga ABC
dengan siku-siku berada di B dan memiliki sisi berturut-turut AB, BC dan AC. Selain
itu segitiga diatas juga memiliki tiga buah sudut yang berada di titik A, B dan
C. Sudut yang menjadi perhatian adalah sudut lancip pada segitiga siku-siku tersebut,
yaitu ∠A
dan ∠C.
Adapun hubungan perbandingan antara sudut lancip dan sisi-sisi
segitiga siku-siku ABC akan dikenal dengan istilah sinus (sin), cosinus (cos),
tangen (tan), cosecan (csc), secan (sec), dan cotangen (cot). Sekarang kita
cari perbandingan sudut lancip A yang
besarnya α dengan sisi-sisi segitiga siku-siku ABC. Adapun
definisi dari perbandingan tersebut yakni sebagai berikut.
a) sinus (sin)
suatu sudut didefinisikan sebagai perbandingan panjang sisi di depan sudut
dengan sisi miring, ditulis sin α =
BC/AC = a/b
b) cosinus
(cos) suatu sudut didefinisikan sebagai perbandingan panjang sisi di samping
sudut dengan sisi miring, ditulis cos α
= AB/AC = c/b
c) tangen (tan) suatu sudut didefinisikan
sebagai perbandingan panjang sisi di depan sudut dengan sisi di samping sudut,
ditulis tan α =BC/AB = a/c
d) cosecan (csc) suatu sudut didefinisikan
sebagai panjang sisi miring dengan sisi di depan sudut, ditulis csc α = AC/BC =
b/a = 1/sin α
e) secan (sec) suatu sudut didefinisikan sebagai
perbandingan panjang sisi miring dengan sisi di samping sudut, ditulis sec α =
AC/AB = b/c = 1/cos α
f) cotangen (cot) suatu sudut didefinisikan
sebagai perbandingan sisi di samping sudut dengan sisi di depan sudut, ditulis
cot α = AB/BC = a/c = 1/tan α
Jika diperhatikan aturan perbandingan di atas,
konsep matematika lain yang perlu diingat kembali adalah teorema Phytagoras. Selain itu, pengenalan akan sisi miring, sisi
di samping sudut, dan sisi di depan sudut tentunya dapat mudah diperhatikan.
Contoh
Soal
Diberikan segitiga siku-siku ABC, siku-siku di ∠ABC.
Jika Panjang sisi AB = 3 cm, BC = 4 cm. Tentukanlah sin A, cos C, dan
tan A.
Penyelesaian:
Jika digambarkan maka segitiga diatas akan
tampak seperti gambar di bawah ini.
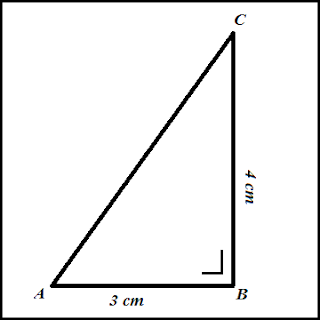
Kita harus mencari panjang sisi miring (AC)
terlebih dahulu dengan menggunakan teorema phytagoras yakni:
AC = √(AB2 + BC2)
AC = √(32 + 42)
AC = √25
AC = 5 cm
sin A = sisi depan/sisi miring
sin A = BC/AC
sin A = 4/5
sin A = 0,8
cos A = sisi samping/sisi miring
cos A = AB/AC
cos A = 3/5
cos A = 0,6
tan A = sisi depan/sisi samping
tan A = BC/AB
tan A = 4/3
Dengan memahami konsep perbandingan trigonometri
pada suatu segitiga siku-siku kita akan mudah memahami aturan sinus dan cosinus
pada segitiga.
0 Response to "Perbandingan Trigonometri Pada Segitiga Siku-Siku"
Posting Komentar
Terima kasih sudah membaca blog ini, silahkan tinggalkan komentar dengan sopan dan tidak mengandung unsur SARA atau pornografi serta tidak ada link aktif. Mohon maaf kalau komentarnya dibalas agak lambat. Kolom komentar ini kami moderasi, jadi kalau ada komentar yang tidak sesuai dengan ketentuan tidak akan dipublikasikan.