Dalam materi ruang tiga dimensi tidak pernah
terpisahkan dengan konsep titik, garis dan bidang. Konsepnya berurutan dimulai
dengan konsep titik, kemudian garis, lalu bidang dan terakhir konsep ruang.
Jika Anda mempelajari konsep ruang maka anda harus menguasai konsep bidang.
Konsep bidang akan anda kuasai jika anda sudah paham dengan konsep garis.
Konsep garis ini juga akan anda kuasai jika anda juga sudah paham dengan konsep
titik. Jadi konsep titik ini merupakan konsep paling dasar dalam mempelajari
konsep ruang tiga dimensi. Jadi Mafia Online sarankan sebaiknya Anda
mempelajarinya dari konsep dasar terlebih dahulu baru lanjut ke konsep
berikutnya.
Oke sekarang kita akan bahas satu persatu konsep
tersebut. Mulai dari konsep titik, garis, dan bidang.
Titik
Kita tidak asing dengan istilah titik. Bahkan
setiap kita menulis kita selalu menggunakannya. Apakah sama titik dalam “dunia
menulis” dengan titik dalam “dunia matematika”?
 |
| Bintang dapat dianggap sebagai titik |
Garis
Oke,
sekarang kita akan bahas mengenai garis. Garis adalah himpunan titik-titik yang
anggotanya terdiri dari lebih dari satu buah titik. Titik-titik tersebut
berderet ke kedua arah yang berlawanan sampai jauh tak terhingga. Model atau
representasi suatu garis misalnya seperti seutas benang atau tali lurus yang
dapat diperpanjang kedua arah yang berlawanan sampai jauh tak terhingga. Garis
hanya mempunyai ukuran panjang. Berbeda dengan titik yang diberi nama
menggunakan satu buah huruf kapital, sedangkan garis diberi nama dengan
menggunakan huruf kecil seperti g, h, k, dan seterusnya, atau dua buah huruf
kapital seperti AB, AC, BC, dan seterusnya. Pada gambar di bawah ini
diperlihatkan dua buah garis, yaitu garis h dan garis AB.
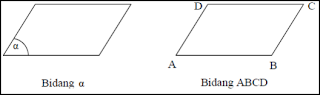
Bidang
Bidang adalah himpunan garis-garis yang anggotanya terdiri dari lebih dari dua buah
garis. Jadi, pada sebuah bidang, terdiri dari banyak sekali garis. Model sebuah
bidang adalah permukaan sebuah kertas yang dapat diperlebar ke semua arah.
Bidang mempunyai ukuran panjang dan lebar serta diberi nama dengan menyebutkan
titik-titik sudut dari bidang tersebut atau memakai huruf α, β, γ , dan seterusnya.
Pada gambar di bawah ini diperlihatkan dua buah bidang, yaitu bidang α dan
bidang ABCD.
Demikian
konsep titik, garis dan bidang. Dari pengertian titik, garis, dan bidang akan memunculkan aksioma atau postulat tentang titik, garis dan bidang yaitu:
=>Melalui dua buah titik sembarang yang tidak berimpit hanya dapat dibuat satu garis lurus
=>Melalui tiga titik sembarang, hanya dapat dibuat satu buah bidang.
=>Melalui satu titik dan garis yang tidak melewati titik tersebut dapat dibuat sebuah bidang
=>Melalui dua buah garis sejajar atau garis yang saling berpotongan dapat dibuat sebuah bidang.
=>Jika suatu garis dan suatu bidang mempunyai dua titik persekutuan, maka garis itu seluruhnya terletak pada bidang.
Nah aksioma-aksioma di atas penting untuk anda pahami untuk memahami materi berikutnya yaitu menggambar irisan bidang pada bangun ruang. Semoga konsep ini membantu Anda dalam mempelajari konsep-konsep berikutnya di materi ruang dimensi tiga. Sekarang bagaimana kedudukan suatu titik terhadap garis dan titik terhadap bidang.
=>Melalui dua buah titik sembarang yang tidak berimpit hanya dapat dibuat satu garis lurus
=>Melalui tiga titik sembarang, hanya dapat dibuat satu buah bidang.
=>Melalui satu titik dan garis yang tidak melewati titik tersebut dapat dibuat sebuah bidang
=>Melalui dua buah garis sejajar atau garis yang saling berpotongan dapat dibuat sebuah bidang.
=>Jika suatu garis dan suatu bidang mempunyai dua titik persekutuan, maka garis itu seluruhnya terletak pada bidang.
Nah aksioma-aksioma di atas penting untuk anda pahami untuk memahami materi berikutnya yaitu menggambar irisan bidang pada bangun ruang. Semoga konsep ini membantu Anda dalam mempelajari konsep-konsep berikutnya di materi ruang dimensi tiga. Sekarang bagaimana kedudukan suatu titik terhadap garis dan titik terhadap bidang.


kurang banyak contohnya....konsepnya juga bisa diperluas
BalasHapusMakasih banget, ada yang ngepost ini. Laporan gue jadi ke tolong <3
BalasHapus