Materi tentang kesebangunan sudah admin bahas pada postingan sebelumnya, silahkan baca terlebih dahulu pengertian kesebangunan pada bangun datar dan syarat dua segitiga yang sebangun. Dua konsep tersebut penting sekali untuk dikuasai agar bisa memahami contoh soal dan pembahasan kesebangunan pada trapesium di bawah ini.
Contoh Soal 1
Perhatikan
gambar trapesium ABCD di bawah ini.
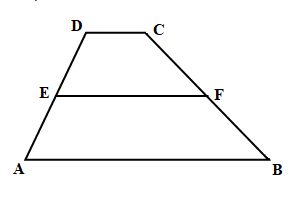 |
| Trapesium ABCD |
a.
Tunjukan bahwa DE/AE = CF/BF
b.
Jika panjang DA = 18 cm, CF = 12 cm, dan FB = 15 cm, tentukan panjang DE dan AE.
c.
Jika panjang DC = 15 cm, CF = 12 cm, FB = 15 cm dan AB = 33 cm, Tentukan
panjang EF.
Penyelesaian:
Untuk
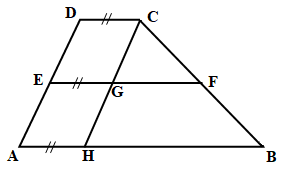
memudahkan mengerjakan soalnya, kita tarik garis dari titik C ke titik H yang
berada digaris AB, sehingga garis CH sejajar dan sama panjang dengan garis AD.
Jika digambarkan akan tampak seperti gambar di bawah ini.
 |
a.
Perhatikan ΔBCH yang sebangun dengan ΔGFC dengan DE = CG dan AE = GH, sehingga akan berlaku:
CH/CG=BC/CF
(CG+GH)/CG
= (CF+BF)/CF
CF.(CG+GH)
= CG.(CF+BF)
CF.CG + CF.GH = CG.CF + CG.BF
CF.GH
= CG.BF
CF.AE
= DE.BF
CF/BF
= DE/AE
DE/AE
= CF/BF (terbukti)
b.
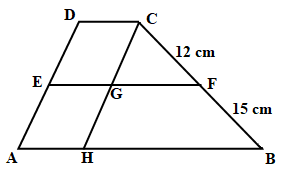
AD = 18 cm, CF = 12 cm, BF = 15 cm. Jika digambarkan akan tampak seperti gambar
di bawah ini.
 |
Dengan
menggunakan persamaan kesebangunan yaitu:
DE/EA
= CF/BF
Dalam
hal ini DE = AD – AE, sehingga persamaannya menjadi:
(AD
– AE)/AE = CF/BF
(18
– AE)/AE = 12/15
(18
– AE)/AE = 4/5
5(18
– AE) = 4.AE
5(18)
– 5AE = 4AE
5(18)
= 4AE + 5AE
5(18)
= 9AE
5(2)
= AE
AE
= 10 cm
Panjang
DE yakni:
DE
= AD – AE
DE
= 18 cm – 10 cm
DE
= 8 cm
Jadi
panjang DE dan AE adalah 8 cm dan 10 cm.
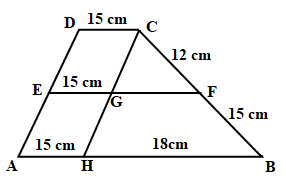
c. DC = 15 cm, CF = 12 cm, BF = 15 cm, AB = 33 cm. Jika di gambarkan akan tampak seperti gambar di bawah ini.
 |
Sekarang
perhatikan Δ BCH yang sebangun dengan ΔGFC, sehingga berlaku persamaan kesebangunan
yakni:
BH/FG
= BC/CF
18/FG
= 27/12
18/FG
= 9/4
2/FG
= 1/4
FG
= 8 cm
Panjang
EF yakni:
EF
= EG + FG
EF
= 15 cm + 8 cm
EF
= 23 cm
Jadi
panjang EF adalah 23 cm
Contoh Soal 2
Perhatikan gambar trapesium ABCD di bawah ini.
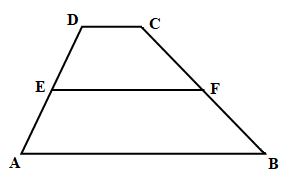 |
Jika
DC//EF//AB dengan AE : DE = 3 : 2. Jika panjang AB = 35 cm dan DC = 10 cm,
tentukan panjang EF.
Penyelesaian:
Jika diilustrasikan soal di atas maka akan tampak seperti gambar di bawah ini.
 |
Perhatikan
ΔBCH yang sebangun dengan ΔGFC. DC = EG = AH, DE = CG, dan AD = CH.
Jika
AE : DE = 3 : 2, maka perbandingan panjang AD = AE + DE = 3 + 2 = 5, sehingga
DE : AD = 2 : 5
atau
DE/AD
= 2/5
Perhatikan
kembali ΔBCH dan ΔGFC, akan berlaku:
CG/CH
= FG/BH
DE/AD
= FG/BH
2/5
= FG/25
2x25
= 5xFG
2
x 5 = FG
FG
= 10 cm
Panjang
EF yakni:
EF
= EG + FG
EF
= 10 cm + 10 cm
EF
= 20 cm
Jadi
panjang EF adalah 20 cm.
Demikian artikel tentang contoh soal dan pembahasan kesebangunan pada trapesium, lengkap dengan gambar ilustrasinya. Jika ada kendala atau permasalahan dalam memahami contoh soal dan pembahasan materi ini, silahkan tanyakan di kolom komentar.
0 Response to "Contoh Soal dan Pembahasan Kesebangunan Pada Trapesium"
Posting Komentar
Terima kasih sudah membaca blog ini, silahkan tinggalkan komentar dengan sopan dan tidak mengandung unsur SARA atau pornografi serta tidak ada link aktif. Mohon maaf kalau komentarnya dibalas agak lambat. Kolom komentar ini kami moderasi, jadi kalau ada komentar yang tidak sesuai dengan ketentuan tidak akan dipublikasikan.