Sebelum lebih lanjut membahas tentang cara mencari jari-jari lingkaran jika yang diketahui sudut pusat dan luas juring. Terlebih dahulu kamu harus paham dengan pengertian sudut pusat dan luas juring. Jika belum paham, silahkan baca postingan Mafia Online sebelumnya yang berjudul “Unsur-Unsur/Bagian-Bagian Lingkaran”.
Pada postingan sebelumnya Mafia Online sudah pernah membahas tentang hubungan sudut pusat dengan luas juring lingkaran. Pada postingan tersebut dijelaskan tentang bagaimana mencari luas juring jika yang diketahui jari-jari lingkaran dan sudut pusat.
Nah pada postingan kali ini Mafia Online akan membahas tentang cara mencari jari-jari lingkaran jika yang diketahui sudut pusat dan luas juring. Perhatikan gambar di bawah ini.
 |
| Juring AOB |
Gambar di atas merupakan sebuah lingkaran berjari-jari r dengan
juring AOB dan sudut pusat α. Seperti yang kita ketahui hubungan antara sudut
pusat (α), luas juring (L.AOB) dan luas lingkaran (L.O) dapat dituliskan dengan
persamaan:
L.O/360° = L.AOB/α
Langkah pertama, untuk mencari jari-jari lingkaran jika
yang diketahui sudut pusat dan luas juring adalah mencari luas lingkaran dengan
menggunakan persamaan:
L.O = (L.AOB/α) x 360° . . . . . .
pers (1)
Langkah kedua, setelah didapatkan luas lingkaran maka
cari jari-jari lingkaran dengan menggunakan rumus:
L.O = πr2
r2 = L.O/π
r = √(L.O/π) . . . . . pers (2)
Jika persamaan 2 disubstitusikan ke persamaan 1, maka
diperoleh:
r = √([(L.AOB/α) x 360°]/π)
r = √(L.AOBx360°/(απ))
dengan:
r = jari-jari lingkaran
L.AOB = juring lingkaran AOB
α = sudut pusat (dalam derajat)
π = 3,14 atau 22/7
360° = sudut satu lingkaran penuh
Untuk memantapkan pemahaman kamu tentang cara mencari
jari-jari lingkaran jika yang diketahui sudut pusat dan luas juring lingkaran,
silahkan simak contoh soal di bawah ini.
Contoh
Soal 1
Luas sebuah juring lingkaran dengan sudut pusat 50
derajat adalah 770 cm2. Tentukan panjang jari-jari lingakaran
tersebut (π = 22/7)!
Penyelesaian:
Jika soal di atas diiluastrasikan ke dalam gambar akan
tampak seperti gambar di bawah ini.
 |
| Juring AOB dengan sudut pusat 50° |
Cari terlebih dahulu luas lingkaran dengan menggunakan
rumus:
L.O = (L.AOB/α) x 360°
L.O = (770/50°) x 360°
L.O = 5544 cm2
Sekarang cari jari-jari lingkaran dengan menggunakan
rumus (π = 22/7):
r = √(L.O/π)
r = √(5544/(22/7))
r = √1764
r = 42 cm
Jadi panjang jari-jari lingkaran tersebut adalah 42 cm.
Contoh
Soal 2
Perhatikan gambar di bawah ini.
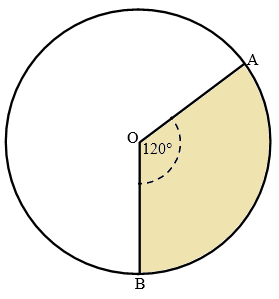 |
| Juring lingkaran AOB dengan sudut pusat 120° |
Jika luas juring AOB = 462 cm2, hitunglah luas
lingkaran dan panjang jari-jari lingkaran tersebut (π = 22/7)!
Penyelesaian:
Luas lingkaran dapat dicari dengan menggunakan rumus:
L.O = (L.AOB/α) x 360°
L.O = (462/120°) x 360°
L.O = 1386 cm2
Panjang jari-jari lingkaran dapat dicari dengan
menggunakan rumus:
r = √(L.O/π)
r = √(1386/(22/7))
r = √441
r = 21 cm
Jadi luas lingkaran dan panjang jari-jari lingkaran
tersebut adalah 1386 cm2 dan 21 cm.
Demikian artikel tentang cara mencari jari-jari lingkaran jika diketahui sudut pusat dan luas juring lingkaran lengkap dengan langkah-langkah dan contoh soal serta penyelesaiannya. Mohon maaf jika ada kata atau tulisan yang salah. Tunggu artikel selanjutnya tentang cara mencari jari-jari lingkaran jika yang diketahui sudut pusat dan panjang busur lingkaran.
Terimakasih sudah ngasih tau rumusnya kak 😁😁🙏🏻
BalasHapus