Menentukan Jarak Terjauh pada Sumbu-X pada Gerak Parabola

Pada postingan sebelumnya Mafia Online sudah membahas tentang menentukan waktu untuk mencapai tinggi maksimum pada gerak parabola, menentukan tinggi maksimum pada gerak parabola dan menentukan waktu untuk mencapai jarak (jangkauan) terjauh pada gerak parabola. Nah pada postingan kali ini Mafia Online akan membahas tentang cara menentukan jarak terjauh di sumbu X pada gerak parabola.

 

Perhatikan gambar di bawah ini.

Pada gerak parabola seperti gambar di atas, titik terjauh terjadi pada titik B. Pada postingan sebelumnya sudah dibahas tentang bagaimana cara menentukan waktu untuk mencapai jarak terjauh pada gerak parabola. Untuk menentukan waktu mencapai jangkauan terjauh dapat menggunakan rumus:

 

t = 2v_o sin α/g

 

kecepatan pada arah sumbu-x tetap dengan persamaan:

x = v_x.t

 

dalam hal ini nilai v_x = v_o cos α, maka:

x = v_o cos α.t

 

Selanjutnya substitusi t pada persamaan:

x = v_o cos α.t

x = v_o cos α. 2v_o sin α/g

x = v_o² (2cos α. sin α)/g

 

dalam hal ini 2cos α. sin α = sin 2α, maka:

x = v_o² sin 2α/g

 

Jadi rumus untuk menentukan jarak terjauh pada sumbu x yakni:

 

x = v_o² sin 2α/g

 

Untuk memantapkan pemahaman kamu tentang materi ini, silahkan simak contoh soal di bawah ini.

 

Contoh Soal 1

Peluru ditembakkan dari sebuah senapan yang mampu memberikan kecepatan awal 50 m/s. Peluru diarahkan dengan sudut 45° terhadap horisontal. Jika percepatan gravitasi ditempat tersebut 10 m/s², tentukan jangkauan terjauh peluru tersebut.

 

Jawab:

v_o = 50 m/s

α = 45°

g = 10 m/s²

 

Untuk mengerjakan soal ini bisa menggunakan 2 cara yakni:

 

Cara 1

Cari terlebih dahulu waktu yang dicapai oleh peluru pada jarak terjauh yakni:

t = 2v_o sin α/g

t = 2(50) sin 45°/10

t = 100 . ½ √2/10

t = 5√2 s

 

sekarang cari jangkauan terjauh dengan menggunakan persamaan:

x = 50 cos 45°. 5√2

x = 50 . ½ √2. 5√2

x = 250 m

 

Cara 2

Untuk cara yang kedua ini dapat menggunakan rumus:

x = v_o² sin 2α/g

x = 50² sin 2(45°)/10

x = 2500 sin 90°/10

x = 250 m

 

Contoh Soal 2

Sebutir peluru ditembakkan dari sebuah senapan yang dapat memberikan kecepatan awal 40 m/s dari puncak menara setinggi 140 m dengan arah membentuk sudut 30° terhadap garis mendatar. Tentukan jarak terjauh peluru tersebut saat tiba di tanah dihitung dari dasar menara!

 

Jawab:

v_o = 40 m/s

y = - 140 m

α = 30°

g = 10 m/s²

 

Jika kita gambarkan akan terlihat seperti gambar di bawah ini.

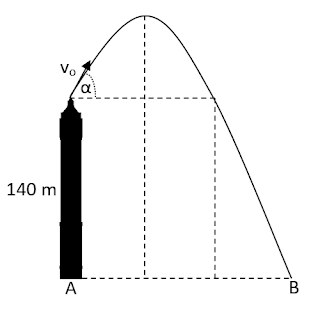
Untuk mencari jangkauan terjauh (titik A ke B) terlebih dahulu harus cari waktu yang diperlukan oleh peluru dari titik A ke titik B dengan menggunakan persamaan gerak parabola yakni:

 

y = v₀ sinα . t – ½ gt²

- 140 = 40 sin 30° . t – ½ (10) t²

- 140 = 20t – 5t²

5t² – 20t – 140 = 0

t² – 4t – 28 = 0

 

Untuk mencari nilai t dapat menggunakan rumus abc yakni:

t = [- b ± √(b² – 4ac)]/2a

t = [- (-4) ± √(4² – 4.1.-28)]/2.1

t = [4 ± √(16 + 112)]/2

t = (4 ± √128)/2

t = (4 ± 11,3)/2

 

t₁ = (4 + 11,3)/2

t₁ = (15,3)/2

t₁ = 7,65 s

 

t₂ = (4 - 11,3)/2

t₂ = - 7,3/2

t₂ = - 3,65 s (tidak mungkin waktu negatif)

Jadi waktu untuk mencapai jarak terjauh adalah 7,65 s

 

Sekarang cari jarak terjauh dengan menggunakan rumus gerak parabola maka:

x = v_o cos α . t

x = 40 cos 30° . 7,65

x = (40)(0,87).(7,65)

x = 266,22 m

Jadi jarak terjauh yang dicapai oleh peluru adalah 266,22 meter.

 

Contoh Soal 3

Sebuah senapan ditembakkan sehingga pelurunya melesat dengan kecepatan awal 100 m/s dari puncak menara setinggi 65 m dengan sudut elevasi 37° (sin 37° = 0,6; cos 37° = 0,8) terhadap garis mendatar. Tentukan jangkauan terjauh peluru tersebut saat tiba di tanah dihitung dari dasar menara!

 

Jawab:

v_o = 100 m/s

y = - 65 m

α = 37°

g = 10 m/s²

 

Contoh soal 3 ini mirip seperti contoh soal 2, sehingga untuk mengerjakannya dapat menggunakan persamaan:

y = v₀ sinα . t – ½ gt²

- 65 = 100 sin 37° . t – ½ (10) t²

- 65 = 60t – 5t²

5t² – 60t – 65 = 0

t² – 12t – 13 = 0 (faktorkan)

(t – 13)(t + 1) = 0

Ambil nilai t positif, maka:

t – 13 = 0

t = 13 s

 

Sekarang cari jarak terjauh dengan menggunakan rumus gerak parabola maka:

x = v_o cos α . t

x = 100 cos 37° . 13

x = (100)(0,8).(13)

x = 1.040 m

Jadi jarak terjauh yang dicapai oleh peluru adalah 1.040 meter.

Share :

Facebook Google+ Twitter

Related Posts :