Cara Cepat Menghitung Panjang Diagonal Sisi dan Diagonal Ruang Kubus

Cara cepat menghitung panjang diagonal sisi dan diagonal ruang kubus sangat penting kamu kuasai, terutama saat mengerjakan soal-soal ruang tiga dimensi khususnya bangun ruang kubus. Misalnya kita disuruh mencari jarak sebuah titik ke salah satu sisi kubus. Jika menggunakan teorema Pytagoras tentunya akan menyita waktu yang cukup lama untuk mengerjakan soal-soal tersebut, sehingga cara cepat perlu dikuasai. Penguasaan cara cepat ini bisa kamu kuasai jika sudah paham konsep dasarnya. Bagaimana cara cepat itu didapatkan?

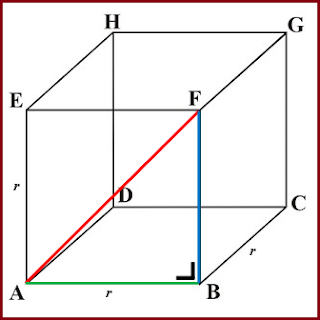
Perhatikan Gambar 1 di bawah ini.

Cara Cepat Menghitung Panjang Diagonal Sisi pada Kubus

Gambar 1

Gambar di atas merupakan sebuah bangun ruang kubus ABCD.EFGH dengan panjang rusuk r. Perhatikan sisi ABFE, garis AF merupakan diagonal sisi atau diagonal bidang. Selain garis AF, masih ada lagi 11 buah diagonal sisi pada kubus ABCD.EFGH yakni AC, BD, EG, FH, BE, CH, DG, BG, CF, AH, dan DE. Bagaimana cara mencari panjang diagonal sisi pada kubus?

Untuk mencari panjang diagonal sisi kubus dapat mengggunakan teorema Pytagoras. Sekarang perhatikan segitiga siku-siku ABF pada kubus ABCD.EFGH di atas. Panjang AF dapat dicari dengan menggunakan teorema Pythagoras yakni:

AF² = AB² + BF²

AF² = r² + r²

AF² = 2r²

AF = √(2r²)

AF = r√2

Jika diagonal sisi atau diagonal bidang dilambangkan dengan d_b, maka rumus untuk mencari diagonal sisi yakni:

d_b = r√2

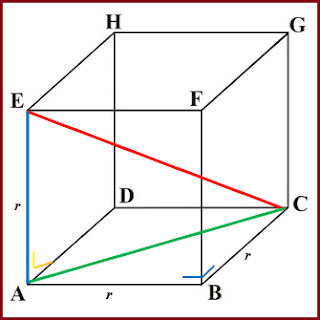
Sekarang perhatikan Gambar 2 di bawah ini!

Cara Cepat Menghitung Panjang Diagonal Ruang Kubus

Gambar 2

Garis CE merupakan salah satu diagonal ruang kubus ABCD.EFGH. Di mana pada bangun kubus ada 4 buah diagonal ruang yang sama panjang yakni AG, CE, BH, dan DF. Bagaimana cara mencari panjang diagonal ruang pada kubus?

Perhatikan segitiga siku-siku ACF pada bangun ruang kubus ABCD.EFGH di atas. Dengan menggunakan Teorema Pytagoras maka panjang CE dapat ditentukan, yakni:

CE² = AE² + AC²

Ingat AC diagonal sisi kubus yang dapat dicari dengan rumus:

d_b = r√2

sehingga menjadi:

CE² = r² + (r√2)²

CE² = r² + 2r²

CE² = 3r²

CE = √(3r²)

CE = r√3

Jika panjang diagonal ruang kubus dilambangkan dengan d_r, maka rumus mencari panjang diagonal ruang pada kubus yakni:

d_r = r√3

Berdasarkan penjelasan di atas maka dapat ditarik kesimpulan, cara cepat untuk mencari panjang diagonal sisi dan diagonal ruang pada kubus dengan panjang rusuk r yakni:

d_b = r√2

dan

d_r = r√3

Cara Cepat Menghitung Panjang Diagonal Sisi dan Diagonal Ruang Kubus

Kubus ABCD.EFGH

Untuk memantapkan pemahaman kamu tentang cara cepat menghitung panjang diagonal sisi dan diagonal ruang, silahkan simak contoh soal di bawah ini.

Contoh Soal

Kubus ABCD.EFGH memiliki rusuk 12 cm, hitunglah panjang diagonal sisi dan panjang diagonal ruang kubus tersebut!

Penyelesaian:

r = 12 cm

Dengan menggunakan cara cepat, panjang diagonal sisi kubus yakni:

d_b = r√2

d_b = (12 cm)√2

d_b = 12√2 cm

Dengan menggunakan cara cepat, panjang diagonal ruang kubus yakni:

d_r = r√3

d_r = (12 cm)√3

d_r = 12√3 cm

Jadi, panjang diagonal sisi dan diagonal ruang kubus tersebut adalah 12√2 cm dan 12√3 cm.

Demikian artikel tentang cara cepat menghitung panjang diagonal sisi dan diagonal ruang pada bangun ruang kubus lengkap dengan gambar ilustrasi dan cara mendapatkan rumus cara cepat menghitung panjang diagonal sisi dan diagonal ruang kubus.

0 Response to "Cara Cepat Menghitung Panjang Diagonal Sisi dan Diagonal Ruang Kubus"

Posting Komentar

Terima kasih sudah membaca blog ini, silahkan tinggalkan komentar dengan sopan dan tidak mengandung unsur SARA atau pornografi serta tidak ada link aktif. Mohon maaf kalau komentarnya dibalas agak lambat. Kolom komentar ini kami moderasi, jadi kalau ada komentar yang tidak sesuai dengan ketentuan tidak akan dipublikasikan.