Persamaan Gerak Parabola

Mungkin kamu pernah memerhatikan gerakan bola saat ditendang oleh penjaga gawang untuk di operkan kepada temannya yang ada di posisi depan. Tampak bola tidak bergerak lurus, namun melengkung.

Ternyata lintasan gerak bola yang melengkung terjadi akibat adanya pengaruh gerak dipercepat beraturan pada sumbu vertikal. Gerakan tersebut disebut gerak parabola. Dengan demikian gerak parabola adalah gerak yang lintasannya berbentuk parabola atau melengkung.

Dalam tulisan berjudul Discorces On Two New Sciences, Galileo mengemukakan sebuah ide yang sangat berguna dalam menganalisis gerak parabola. Dia menyatakan bahwa gerak parabola dapat dipandang sebagai perpaduan gerak lurus beraturan pada sumbu horisontal (sumbu x) dan gerak lurus berubah beraturan pada sumbu vertikal (sumbu y) secara terpisah.

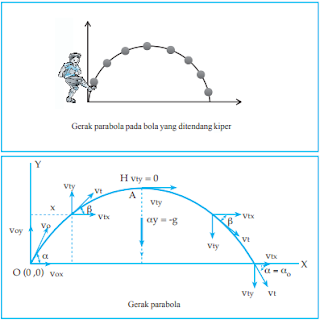sebuah benda yang dilempar dengan kecepatan awal v_o dan sudut kecondongan (sudut elevasi) sebesar α sehingga benda melakukan gerak parabola. Jika kecepatan awal v_o diuraikan pada sumbu x dan sumbu y di dapat v_ox dan v_oy dimana:

v_ox : v_o cos α

v_oy : v_o sin α

Karena gerak pada sumbu x (horizontal) adalah gerak lurus beraturan, maka kecepatan setelah t adalah:

v_tx = v_ox

v_tx = v_o cos α

Perpindahan yang ditempuh setelah t adalah:

x_t = v_ox . t

x_t = v_o cos α . t

Gerak pada sumbu-y (vertikal) adalah gerak lurus berubah beraturan, karena benda mengalami perubahan kecepatan akibat percepatan gravitasi Bumi. Dalam hal ini, arah gerak benda vertikal ke atas sehingga persamaan kecepatan geraknya pada setiap titik adalah:

v_ty = v_0y – gt

Dalam hal ini v_0y = v₀ sinα , maka:

v_ty = v₀ sinα – gt

Kecepatan benda saat t merupakan resultan dari kecepatan benda pada arah sumbu x dan kecepatan benda pada arah sumbu y, sehingga kecepatan benda saat t yakni:

v = √(v_tx² + v_ty²)

Posisi benda pada sumbu-y (menurut ketinggian) dapat dituliskan dengan persamaan berikut:

y_t = v_0y . t – ½ gt²

atau

y_t = v₀ sinα . t – ½ gt²

 

Untuk memantapkan pemahaman kamu tentang materi persamaan gerak parabola, silahkan simak contoh soal di bawah ini.

Contoh Soal

Sebuah peluru ditembakkan dari permukaan tanah dengan kecepatan awal 100 m/s dengan sudut elevasi 37° (sin 37° = 0,6; cos 37° = 0,8). Jika g = 10m/s², maka tentukan kecepatan dan posisi bola pada 1 sekon pertama!

Jawab:

v₀ = 100 m/s

g = 10 m/s²

α = 37°

Kecepatan pada t = 1s memenuhi:

v_tx = v_o cos α

v_tx = 100 cos 37°

v_tx = 100 . 0,8

v_tx = 80 m/s

v_ty = v₀ sinα – gt

v_ty = 100 sin 37° – 10.1

v_ty = 100.0,6 – 10

v_ty = 50 m/s

v = √(v_tx² + v_ty²)

v = √(80² + 50²)

v = √(6400 + 2500)

v = √8900

v = 94,34 m/s

Jadi kecepatan  peluru pada saat 1 sekon pertama adalah 94,34 m/s

 

posisi pada t = 1 s memenuhi:

x_t = v_o cos α . t

x_t = 100 cos 37° . 1

x_t = 100 . 0,8 . 1

x_t = 80 m

y_t = v₀ sinα . t – ½ gt²

y_t = 100 sin 37° . 1 – ½ 10. 1²

y_t = 100 . 0,6 . 1 – 5

y_t = 55 m

Jadi posisi peluru pada saat 1 sekon pertama adalah r = (x_t, y_t) = (80, 55) m

 

Untuk melatih kemampuan kamu tentang materi persamaan parabola ini, silahkan kerjaka soal latihan di bawah ini.

Soal Latihan

Sebuah benda ditembakkan dengan kecepatan awal 50 m/s dan sudut elevasi 53°  (sin 53° = 0,8; cos 53° = 0,6 ). Tentukan kecepatan dan posisi benda pada saat t = 4s!

Share :

Facebook Google+ Twitter

Related Posts :