Sebelumnya Mafia Online sudah
membahas tentang kecepatan sesaat dalam satu dimensi, serta beberapa contoh
soalnya juga sudah dibahas pada postingan tersebut. Postingan kali ini akan
membahas tentang kecepatan sesaat dalam dua dimensi. Untuk lebih memudahkan
memahami konsep ini, admin gunakan cara turunan fungsi vektor posisi untuk
mencari kecepatan sesaat. Sekarang perhatikan gambar di bawah ini.
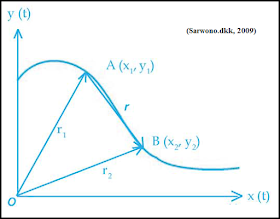 |
| Partikel bergerak dalam bidang xy |
Sebuah partikel bergerak dari posisi
r1 ke posisi r2 pada bidang xy dengan posisi r merupakan
resultan antara posisi x(t) dan y(t). Sebelumnya pada kecepatan sesaat dalam
satu dimensi menggunakan konsep turunan untuk mencari kecepatan sesaatnya, maka
pada kecepatan sesaat dalam dua dimensi juga berlaku hal yang sama, maka:
v
= dr/dt
karena dalam dua dimensi maka r = xi + yj
sehingga persamaannya menjadi:
v
= d(xi + yj)/dt
v
= (dx/dt)i + (dy/dt)j
sedangkan besarnya kecepatan sesaat
merupakan nilai mutlak dari v yang ditulis dengan rumus:
I v I = √[(dx/dt)2 +
(dy/dt)2]
Untuk memantapkan pemahaman kamu
tentang materi kecepatan sesaat dalam dua dimensi ini, silahkan simak contoh
soal di bawah ini.
Contoh
Soal 1
Sebuah partikel bergerak dalam
bidang xy dengan persamaan x = t2
+ 4t – 1 dan y = t2 + 2t,
x dan y dalam meter dan t dalam sekon. Tentukan posisi benda, kecepatan sesaat,
dan besar kecepatan pada waktu t = 2 sekon!
Penyelesaian:
Posisi benda dinyatakan dengan r maka:
r
= xi + yj
r
= (t2 + 4t – 1)i + (t2
+ 2t)j
Untuk mencari posisi benda dengan
cara memasukan nilai t = 2 ke persamaan r,
maka:
r
= (t2 + 4t – 1)i + (t2
+ 2t)j
r
= (22 + 4.2 – 1)i + (22
+ 2.2)j
r
= (4 + 8 – 1)i + (4 + 4)j
r
= (11i + 8j) m
Sedangkan untuk mencari kecepatan
sesaat pada saat t = 2, pertama harus menurunkan fungsi x dan fungsi y terhadap
waktu terlebih dahulu sehingga:
Turunan fungsi x:
dx/dt = d(t2 + 4t – 1)/dt
dx/dt = 2t + 4
turunan fungsi y:
dy/dt = d(t2 + 2t)/dt
dy/dt = 2t + 2
maka kecepatan sesaat di t = 2 yakni:
v
= (dx/dt)i + (dy/dt)j
v
= (2t + 4)i + (2t + 2)j
v
= (2.2 + 4)i + (2.2 + 2)j
v
= (8i + 6j) m/s
Besar kecepatan pada saat t = 2
yakni:
I v I = √[(dx/dt)2 +
(dy/dt)2]
I v I = √[(8)2 +
(6)2]
I v I = √(64 + 36)
I v I = √(100)
I v I = 10 m/s
Contoh
Soal 2
Sebuah partikel bergerak pada bidang
xy dengan persamaan x = t2
+ 3 dan y = t – t2, x dan
y dalam meter dan t dalam sekon. Tentukan posisi partikel pada saat t = 3 sekon,
dan vektor kecepataan dan besar kecepatan pada saat t= 2 sekon.
Penyelesaian:
Posisi benda dinyatakan dengan r maka:
r
= xi + yj
r
= (t2 + 3)i + (t – t2)j
Untuk mencari posisi benda dengan
cara memasukan nilai t = 3 ke persamaan r,
maka:
r
= (t2 + 3)i + (t – t2)j
r
= (32 + 3)i + (3 – 32)j
r
= (9 + 3)i + (3 – 9)j
r
= (12i – 6j) m
Sedangkan untuk mencari kecepatan
sesaat pada saat t = 2, harus menurunkan fungsi x dan fungsi y terhadap
waktu terlebih dahulu sehingga:
Turunan fungsi x:
dx/dt = d(t2 + 3)/dt
dx/dt = 2t
turunan fungsi y:
dy/dt = d(t – t2)/dt
dy/dt = 1 – 2t
maka kecepatan sesaat di t = 2 yakni:
v
= (dx/dt)i + (dy/dt)j
v
= (2t)i + (1 – 2t)j
v
= (2.2)i + (1 – 2.2)j
v
= (4i – 3j) m/s
Besar kecepatan pada saat t = 2
yakni:
Ι v I = √[(dx/dt)2 +
(dy/dt)2]
I v I = √[(4)2 +
(– 3)2]
I v I = √(16 + 9)
I v I = √(25)
I v I = 5 m/s
Demikian pembahasan materi dan
contoh soal tentang kecepatan sesaat dalam dua dimensi. Mohon maaf jika ada
kata-kata atau perhitungan yang salah dalam postingan ini. Jika ada kendala
dalam memahami materi ini, silahkan tanyakan pada kolom komentar. Salam mafia
=> kita pasti bisa.
0 Response to "Kecepatan Sesaat Dalam Dua Dimensi"
Posting Komentar
Terima kasih sudah membaca blog ini, silahkan tinggalkan komentar dengan sopan dan tidak mengandung unsur SARA atau pornografi serta tidak ada link aktif. Mohon maaf kalau komentarnya dibalas agak lambat. Kolom komentar ini kami moderasi, jadi kalau ada komentar yang tidak sesuai dengan ketentuan tidak akan dipublikasikan.